[¯|¯] Approssimando la distribuzione dei numeri primi

Luglio 16th, 2019 | by Marcello Colozzo |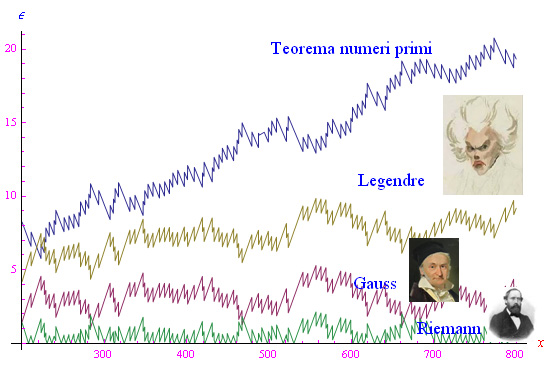

numeri primi,approssimazione,teorema dei numeri primi,riemann
Fig. 1

Ricordiamo che il valore assunto dalla funzione reale π(x) restituisce il numero di primi in [0,x]. Per il teorema dei numeri primi, il comportamento asintotico di tale funzione è simboleggiato da


Legendre trovò un'approssimazione migliore:


Gauss, invece, approssimò la distribuzione con la funzione logaritmo integrale:


Infine Riemann trovò l'approssimazione


dove ζ è la ben nota funzione zeta di Riemann. Con Mathematica possiamo graficare l'errore


per le singole approssimazioni, ottenendo il grafico di fig. 1.

No TweetBacks yet. (Be the first to Tweet this post)

Tags: , , ,

Articoli correlati

Commenta l'esercizio