[¯|¯] Spettro di potenza di un'onda quadra
Giugno 28th, 2018 | by Marcello Colozzo |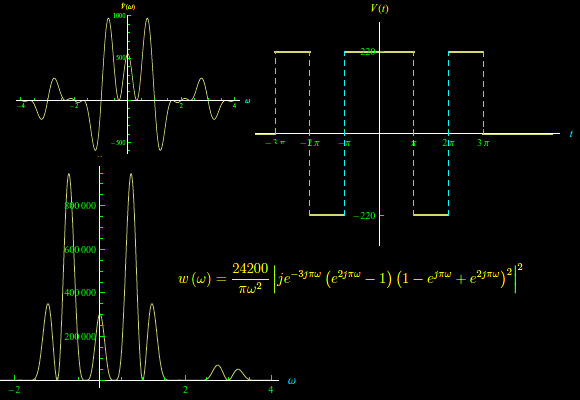
Ricapitoliamo, correggendo, i risultati dell' esercizio precedente. Stiamo considerando una resistenza ohmica R sottoposta a una d.d.p. di durata τ:
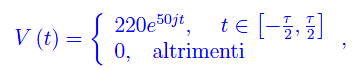
calcolandone la trasformata di Fourier:
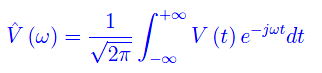
La potenza istantanea dissipata per effetto Joule è
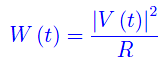
Denotando con E(t) l'energia dissipata all'istante t, si ha:
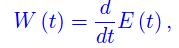
onde
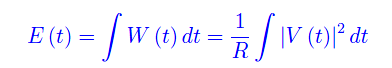
In particolare, l'energia totale dissipata è:
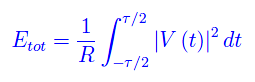
Più in generale, i.e. per una qualunque V(t) di modulo quadro sommabile in (-oo,+oo), si ha
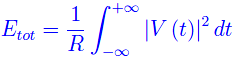
Per l'uguaglianza di Parseval
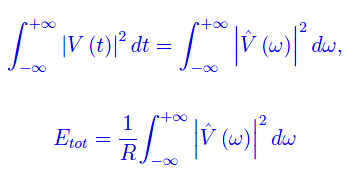
Introducendo lo spettro di potenza:
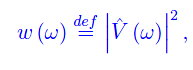
si ha
La funzione di autocorrelazione è definita dalla coppia di trasformate integrali:
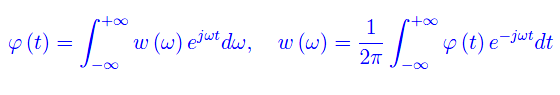
Segue
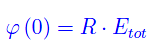
Tutto ciò suggerisce:
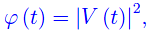
L'espressione corretta è
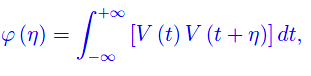
dove η definisce un intervallo di tempo. Consideriamo ora l'esempio di una d.d.p. con un andamento del tipo onda quadra:
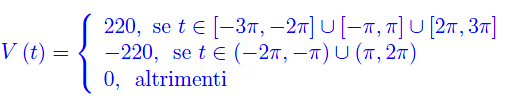
La trasformata di Fourier è:
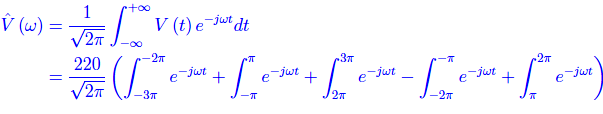
Gli integrali si calcolano facilmente:
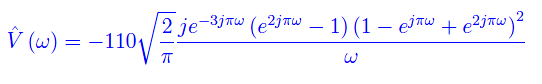
Lo spettro di potenza
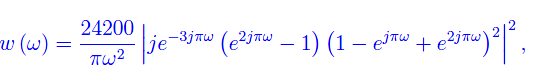
i grafici sono riportati in fig. 1.
Sostienici
Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.
No TweetBacks yet. (Be the first to Tweet this post)
Tags: onda quadra, spettro di potenza, Trasformata di Fourier
Articoli correlati
Congettura di Riemann
Trasformata discreta di Fourier
Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier 
Infinitesimi ed infiniti
Limiti notevoli
Punti di discontinuità
Misura di Peano Jordan
Eserciziario sugli integrali
Differenziabilità 
Differenziabilità (2)
Esercizi sui limiti
Appunti sulle derivate
Studio della funzione
Esercizi sugli integrali indefiniti
Algebra lineare
Analisi Matematica 2
Analisi funzionale
Entanglement quantistico
Spazio complesso
Biliardo di Novikov
Intro alla Meccanica quantistica
Entanglement Quantistico
