» Esercizi svolti di Matematica e Fisica

[¯|¯] Il vettore definito come classe di equivalenza

Giugno 1st, 2018 | by Marcello Colozzo |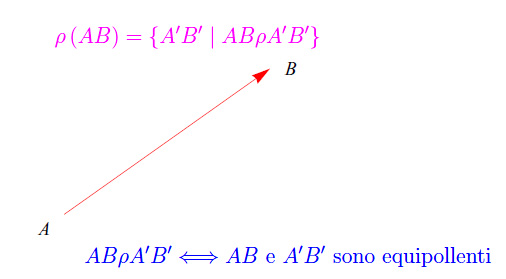

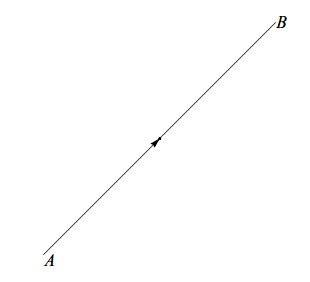
Comunque prendiamo nello spazio ordinario i punti A e B, è univocamente definito il segmento di estremi A e B, che indichiamo con AB. Fissiamo, quindi, un verso di percorrenza che assumiamo essere quello da A verso B, come illustrato in figura:.

Definizione
I segmenti AB e A'B' si dicono congruenti se hanno la stessa lunghezza, cioè se esiste un movimento che muta AB in A'B'.

Una unità di misura individua univocamente la lunghezza di AB, nota come misura assoluta del segmento e che denotiamo con |AB|.
Definizione
I segmenti AB e A'B' si dicono equipollenti se

1. se AB e A'B' sono congruenti;
2. se la retta per A e B (con A distinto da B) è parallela alla retta per A' e B', ovvero se AB e A'B' hanno la stessa direzione;
3. il verso di percorrenza di AB è concorde al verso di percorrenza di A'B'.

Detto S l'insieme dei segmenti dello spazio ordinario R³, consideriamo la seguente relazione ρ (nel senso dell'Algebra

È facile mostrare che ρ verifica la proprietà riflessiva, la proprietà simmetrica e la proprietà transitiva. Quindi ρ è una relazione di equivalenza. Ne consegue il partizionamento di S in classi di equivalenza. Come è noto dall'Algebra, la classe di equivalenza individuata dal segmento AB è l'insieme di tutti e soli i segmenti equipollenti ad AB, cioè:

Definizione
La classe di equivalenza

si dice vettore individuato dal segmento AB.

In altri termini, un vettore è l'ente astratto che accomuna un insieme di segmenti equipollenti. In ciò troviamo un'analogia con la definizione di direzione, quale ente astratto che accomuna un insieme di rette parallele. Nel caso dei vettori abbiamo una condizione più forte, poiché dobbiamo aggiungere la congruenza e il verso di percorrenza dei segmenti.

Graficamente un vettore viene indicato con una freccia orientata da A verso B, come illustrato nella figura al top di questa pagina.

Per quanto precede, una classe di equivalenza è l'insieme dei segmenti equipollenti a un assegnato segmento orientato. Dimostriamo la seguente proposizione:

Proposizione
Ogni classe di equivalenza è costituita da oo³ elementi.

Dimostrazione

Per una assegnata classe di equivalenza, comunque prendiamo un suo elemento, in ogni punto dello spazio ordinario si può costruire un segmento orientato equipollente al predetto elemento. Dal momento che i punti dello spazio ordinario sono oo³, tale sarà il numero di segmenti equipollenti, da cui l'asserto.

Osservazione
Alcuni autori utilizzano la denominazione vettore libero ordinario al posto di quella appena definita.

Sostienici

Tags: relazione di equipollenza, segmenti equipollenti, vettore, vettore libero ordinario

Articoli correlati