[¯|¯] Giocando una partita al Biliardo di Novikov
Novembre 22nd, 2017 | by Marcello Colozzo |
Rileggendo Einstein, passando per gli universi di Gödel per concludere una partita al biliardo di Novikov.
Un articolo sui viaggi nel tempo ha fornito l'input per uno scambio di idee sul principio di autoconsistenza di Novikov.
In un qualunque modello cosmologico lo spaziotempo è incurvato dal campo gravitazionale della materia distribuita nell'universo. Spaziotempo curvo significa in sostanza, linee coordinate curve, incluse quelle temporali.
Per capirci, consideriamo l'esempio banale di una palla di biliardo che si muove lungo una retta che a sua volta, assumiamo come asse x del sistema di riferimento inerziale K da cui osserviamo il moto. Il diagramma spaziotemporale è riportato in figura:
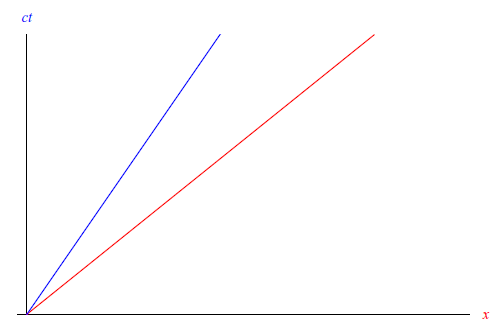
Qui la semiretta blu è la linea di universo della palla di biliardo, mentre la semiretta rossa appartiene alla bisettrice del primo e terzo quadrante, e rappresenta la linea di universo di una particella che si muove alla velocità della luce c, giacché in ordinate riportiamo la grandezza (omogenea ad una distanza) ct, dove t è il tempo misurato dall'orologio di K. Rammentiamo che in Relatività Speciale le particelle che si muovono alla velocità della luce sono massless, ossia hanno massa a riposo nulla.
Dal momento che la linea di universo è una retta, si ha che la biglia si muove a velocità costante v, e deve essere v
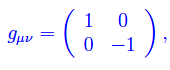
onde ponendo come da convenzione
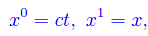
si ha
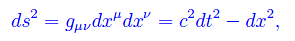
che definisce l'intervallo spaziotemporale tra la coppia di punti infinitamente "vicini":
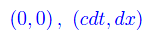
Anche qui notiamo la strana convenzione di scrivere prima l'ordinata e poi l'ascissa, nel senso che le coordinate cartesiane di un generico punto vengono scritte come (ct,x).
È chiaro che non abbiamo un punto nel senso fisico del termine, in quanto una delle coordinate è di tipo temporale. Ciò si esprime dicendo che la coppia ordinata (ct,x) denota un evento (che avviene nel punto di ascissa x al tempo t). Ora immaginiamo che per un qualche processo fisico (gravitazionale, per essere precisi) lo spazio inteso come totalità degli eventi (ct,x) non sia piatto, ma curvo. In un tale spazio le linee coordinate sono incurvate, come illustrato in figura:

Per quanto precede, siamo in presenza di un campo gravitazionale, e nel paradigma della Relatività Generale le componenti del tensore metrico compongono un integrale del seguente sistema di equazioni differenziali non lineari alle derivate parziali e del second'ordine, note come equazioni di Einstein:
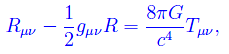
dove Rµν è il tensore di Ricci, dato dalla contrazione del tensore di curvatura di Riemann:
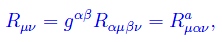
In tutte questo formule gli indici dei vari enti (tensoriali e non) sono del tipo µ=0,1,2,3, mentre noi stiamo considerando il caso 2-dimensionale. Ma tutto ciò non inficia il ragionamento fatto fino ad ora, nel senso che la generalizzazione a 4-dim è immediata. La domanda che ci poniamo è riassunta dal problema:
Problema
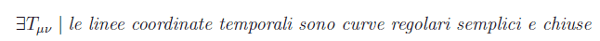
Tali linee coordinate sono note con l'acronimo CTC. Osserviamo innanzitutto che le CTC conducono a una violazione della causalità. Per comprendere ciò sono necessarie alcune premesse: nello spaziotempo il trascorre del tempo è inglobato nella geometria. Ad esempio, riprendiamo il caso della biglia che compie un moto rettilineo ed uniforme, la cui linea di universo è tracciata nel grafico di figura:
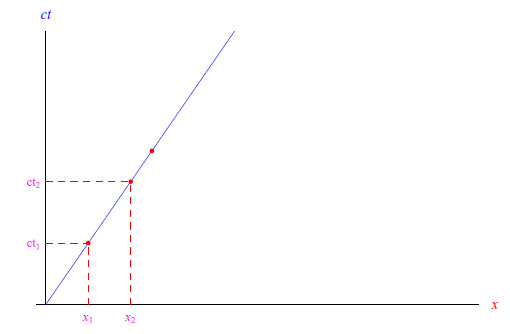
dove (ct1,x1) e (ct2,x2) sono due eventi distinti dello stesso processo fisico (moto della biglia). La dinamica del moto è racchiusa nella linea di universo, nel senso che è come se la biglia fosse splittata in un numero di biglie pari al numero di eventi che compongono la sua linea di universo, ossia infinito non-numerabile. Per dirla in un altro modo, lo spaziotempo è statico e la dinamica dei processi è inglobata nelle linee di universo.
È chiaro che affinché sia valido il principio di causalità (necessario, in quanto stiamo considerando processi deterministici) deve essere verificata la condizione di moto non superluminale. Ma ciò non basta, poiché nel caso in esame deve essere:
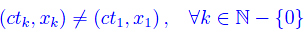
Si noti che tale disuguaglianza è automaticamente verificata in ogni spaziotempo piatto e in ogni spaziotempo curvo privo di CTC. Di contro, l'esistenza di una CTC accoppiata a una linea coordinata spaziale chiusa, implicherebbe:
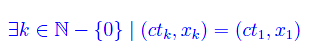
Fisicamente, ciò corrisponde alla situazione in cui la palla di biliardo collide all'istante tk con il suo clone all'istante t1< tk. Ma ciò equivale a dire che la biglia collide con sé stessa nel passato. E ciò è manifestamente una violazione della causalità.
Il caso matematicamente più semplice in cui ciò si verifica è rappresentato da uno spaziotempo 2-dim coindente con la superficie di una sfera di raggio R (che può essere posto pari a 1, ottenendo la sfera S2). Introducendo le usuali coordinate angolari (θ,φ) dove Rθ o meglio il suo complementare, svolge il ruolo di coordinata temporale, mentre Rφ è la coordinata spaziale, si ha il seguente tensore metrico:
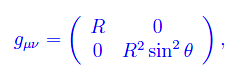
onde
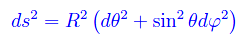
Dal momento che le linee temporali sono i meridiani, si ha che questo tipo di spaziotempo è denso di CTC. Ne consegue che ogni particella collide con sé stessa nel passato. La generalizzazione a 4 dimensioni è immediata.
Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

Tags: biliardo di novikov, ctc, viaggi nel tempo
Articoli correlati



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico









