[¯|¯] Oscillazioni forzate. Risonanza
Marzo 22nd, 2017 | by Marcello Colozzo |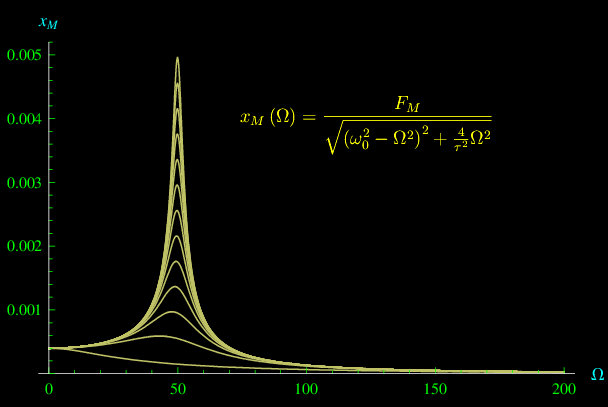
Fig. 1. Ascissa di un oscillatore smorzato sottoposto a una forza funzione sinusoidale del tempo
Abbiamo studiato le oscillazioni forzate in condizioni di idealità, ovvero trascurando le forze di attrito. Nel caso di una sollecitazione esterna funzione sinusoidale del tempo, abbiamo stabilito che se la sua frequenza Ω è di poco inferiore alla frequenza caratteristica ω0 dell'oscillatore, si verifica il fenomeno dei battimenti (che è una conseguenza delle formule di prostaferesi). In particolare, se Ω=ω0 si un battimento di frequenza nulla, ovvero il fenomeno della risonanza.
Consideriamo ora uno scenario più realistico: una forza esterna che sia funzione sinusoidale del tempo, applicata a un oscillatore armonico in presenza di forze viscose. Precisamente:
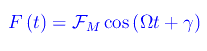
Il secondo principio della dinamica restituisce:
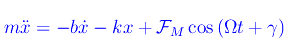
Dividendo primo e secondo membro per la massa m:
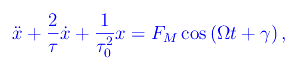
dove
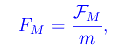
mentre τ e τ0 sono le costanti di tempo introdotte in un post precedente, cioè
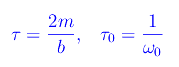
Abbiamo così ottenuto un'equazione differenziale ordinaria del secondo ordine lineare non omogenea. Dalla teoria delle equazioni differenziali sappiamo che il suo integrale generale è:
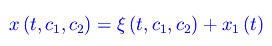
Qui c1 e c2 sono le usuali costanti di integrazione, mentre le funzioni ξ(t,c1,c2) e ξ(t) sono rispettivamente l'integrale generale dell'equazione omegenea associata e un integrale particolare dell'equazione completa. Abbiamo già studiato l'equazione omogenea che descrive le oscillazioni libere nei tre casi:

che in termini di costanti di tempo si scrivono rispettivamente:
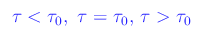
Nelle oscillazioni forzate il caso più interessante è quello oscillatorio smorzato. Ci proponiamo, dunque, di determinare l'equazione oraria di un oscillatore smorzato quando è presente una sollecitazione esterna funzione sinusoidale del tempo. In questo caso, l'integrale generale dell'equazione omogenea è
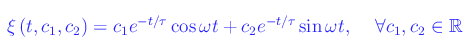
Ricordiamo che
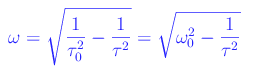
Per determinare l'integrale particalare x1(t) utilizziamo il metodo dei coefficienti indeterminati, scrivendo x1(t) in notazione complessa:
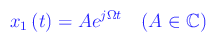
Innanzitutto scriviamo la forza esterna (per unità di massa) in notazione complessa:
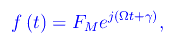
Calcolando poi le derivate prima e seconda della x1(t) e immettendo nell'equazione differenziale:

da cui
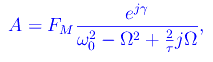
Segue
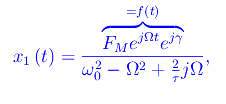
onde:
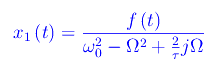
Tuttavia a noi interessa la parte reale della funzione x1(t), quindi sviluppiamo l'ampiezza complessa:
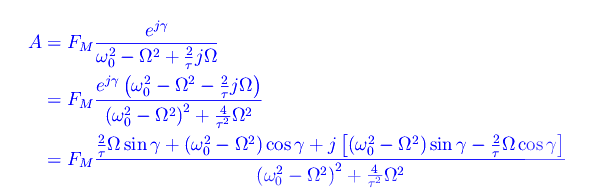
Scrivendo A nella forma A=|A|ejφ, si ha che il modulo |A| si calcola immediatamente dalla seconda delle formule precedenti:

mentre la fase:
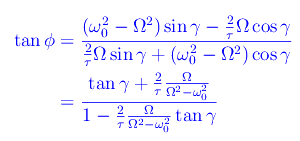
Se poniamo
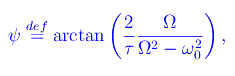
si ha
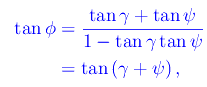
dove abbiamo utilizzato la nota formula di addizione degli archi:
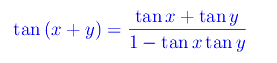
Quindi

A questo punto non dobbiamo fare altro che prendere la parte reale della funzione x1(t) dopo aver immesso tutte le grandezze trovate:
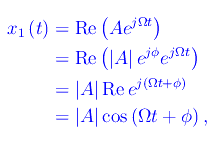
ovvero
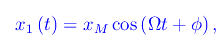
dove xM è l'ampiezza:
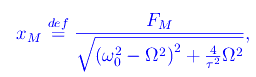
mentre la fase è stata già calcolata. Finalmente possiamo scrivere l'integrale generale dell'equazione differenziale completa:
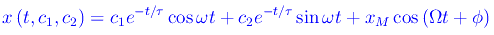
Derivando otteniamo la velocità:
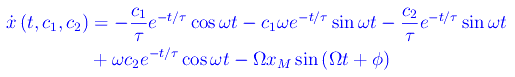
Imponendo le condizioni iniziali
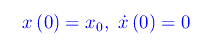
si perviene al sistema lineare
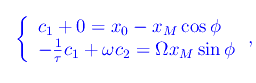
la cui unica soluzione è
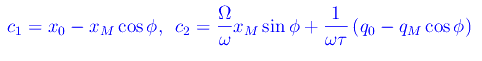
Quindi
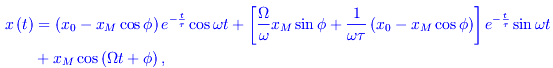
da cui vediamo che x(t) è la somma di due contributi:
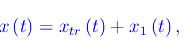
dove xtr(t) è il termine transitorio o transiente, mentre x1(t) è il termine permanente o a regime, ovvero l'integrale particolare trovato in precedenza. Precisamente:
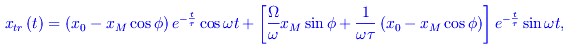
da cui vediamo che non è periodico ma esponenzialmente smorzato e per t»t diviene trascurabile, onde il termine dominante è x1(t). Cioè a regime l'oscillatore oscilla con la stessa frequenza della sollecitazione esterna. Osserviamo che tale circostanza si verifica non solo per b
A regime l'ampiezza delle oscillazioni in funzione della frequenza Ω è
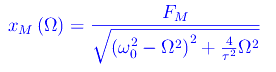
Eseguiamo uno studio di funzione di tale grandezza.
Insieme di definizione
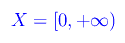
Segno della funzione
È manifestamente
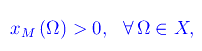
per cui il grafico ΓxM è contenuto nel primo quadrante del piano cartesiano (O&OMega;xM).
Intersezione con l'asse delle ascisse
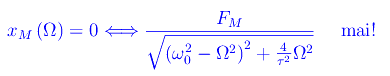
onde non esistono zeri al finito.
Intersezione con l'asse delle ordinate
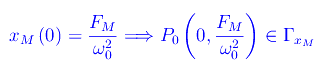
Comportamento agli estremi dell'insieme di definizione
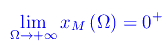
Cioè la funzione è infinitesima
all'infinito o ciò che è lo stesso, l'asse delle ascisse è asintoto orizzontale.
Studio della derivata prima
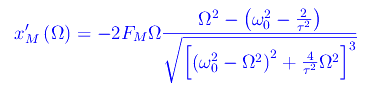
Abbiamo
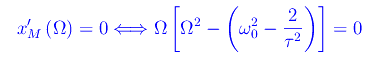
Una delle radici è Ω=0, per cui il grafico della funzione "parte" con tangente orizzontale.
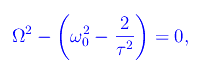
che ammette radici reali se
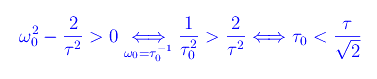
Ricordiamo che la condizione

esprime il caso oscillatorio smorzato, per cui abbiamo trovato una condizione più stringente:

che in termini di coefficiente di viscosità b si scrive
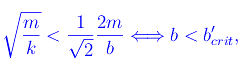
avendo definito un nuovo valore critico di b:

Rammentiamo il valore critico di b che discrimina i comportamenti aperiodico,critico e oscillatorio smorzato:
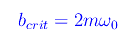
Segue
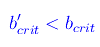
In tale ipotesi l'equazione precedente ammette due radici reali e distinte &Omega0 e -&Omega0, essendo
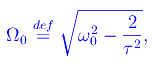
per cui -&Omega0 è da scartare. Inoltre:
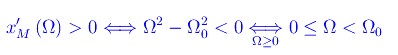
Cioè la funzione xM(Ω) è strettamente crescente per Ω appartenente a(0,Ω0), ed è strettamente decrescente in (Ω0,+oo), onde Ω0 è punto di massimo relativo, ed è facile persuadersi che si tratta di un massimo assoluto. Per quanto detto, se b
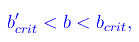
l'ampiezza non ha massimi/minimi per Ω>0 e decresce monotonamente in funzione di Ω, mentre il termine transiente è ancora oscillante. Infine, per b>bcrit il termine transiente non è oscillante e l'ampiezza dell'oscillazione a regime è ancora monotonamente decrescente (in funzione della frequenza della forza esterna). Per una questione di comodità matematica è conveniente esprimere le varie condizioni in termini delle costanti di tempo. Ad esempio:
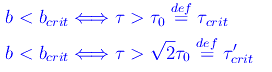
Supponiamo di avere un oscillatore i cui valori m e k siano tali che
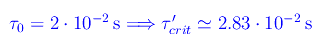
In un esperimento computazionale, siamo liberi di variare il parametro reale positivo τ che è la costante di tempo delle forze di attrito. Per τ=0.015s si ottiene l'andamento di figura:
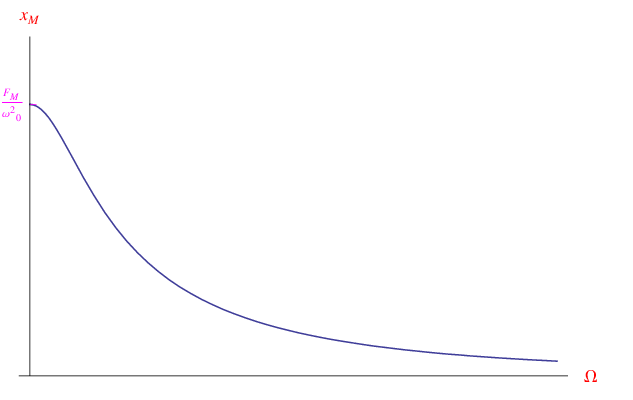
da cui vediamo che non ci sono massimi relativi per valori positivi della frequenza. Aumentando progressivamente la costante di tempo delle forze di attrito, spuntano i primi massimi dell'ampiezza che progressivamente diventano più piccati come mostrato in figura:
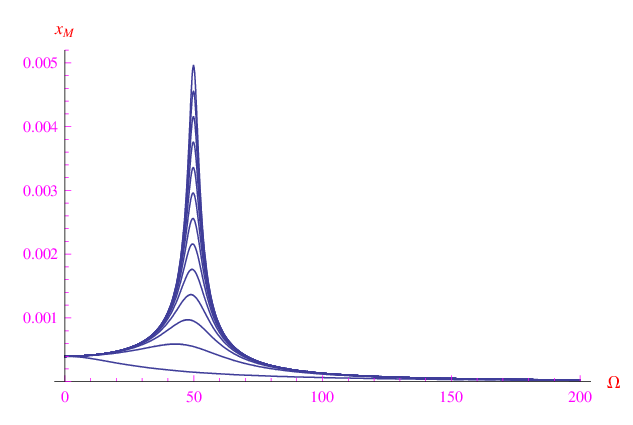
Tags: oscillatore armonico smorzato, oscillazioni forzate, risonanza
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











