[¯|¯] L’integrale di Mengoli-Cauchy e il teorema di Torricelli-Barrow

[¯|¯] L'integrale di Mengoli-Cauchy e il teorema di Torricelli-Barrow

Giugno 1st, 2015 | by Marcello Colozzo |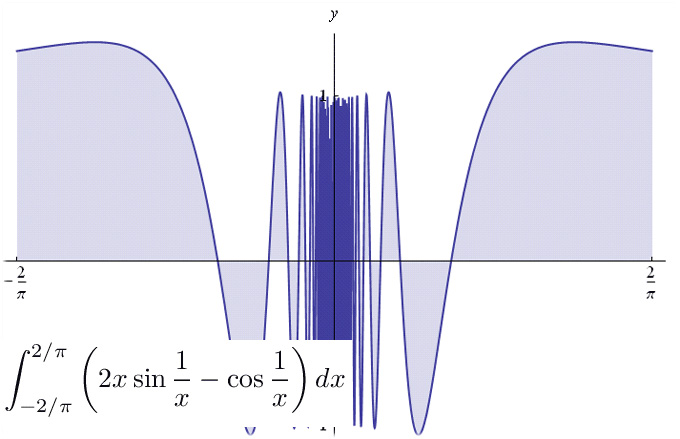

integrale definito, teorema fondamentale del calcolo integrale

In una dispensa precedente abbiamo introdotto la nozione di integrale definito di una funzione continua in un intervallo chiuso e limitato [a,b].
Tale integrale è anche noto in letteratura come l'integrale di Mengoli-Cauchy. Ci si può chiedere se sia possibile estendere tale nozione a funzioni dotate di punti di discontinuità nell'intervallo di integrazione. Nella dispensa di oggi (vedi link più avanti) esaminiamo il comportamento di alcune funzioni non continue in un assegnato intervallo [a,b]. Più precisamente, partiamo dal caso più semplice: funzioni con uno o più punti di discontinuità eliminabili. Ad esempio:

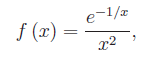
che non è definita in x=0, ma è ivi infinitesima. Quindi ci poniamo il quesito:

discontinuità eliminabili,integrali generalizzati

Calcolando numericamente le somme integrali e facendo tendere a zero l'ampiezza della decomposizione/partizione, si perviene a una risposta affermativa del quesito.

Ne consegue che l'estensione della la definizione a funzioni dotate di punti di discontinuità eliminabili, non presenta alcun problema. Viceversa, i casi più critici sono quelli in cui la funzione integranda presenta uno o più punti di discontinuità di seconda specie nell'intervallo di integrazione. Ad esempio:

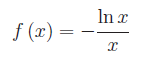
discontinuità di seconda specie,integrali generalizzati

Ripetendo il procedimento di calcolo si giunge alla conclusione:

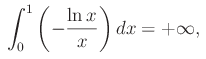
che è un risultato ragionevole, giacchè il corrispondente rettangoloide è illimitato. Ma questa non è una condizione sufficiente per la divergenza dell'integrale. Infatti, l'integrale della funzione:
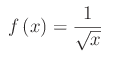
discontinuità di seconda specie,integrali generalizzati

converge.

Un esempio più drammatico è riportato nel grafico della figura al top di questo post. Stiamo parlando dell'integrale esteso a [-2/pi,2/pi] della funzione:

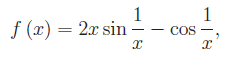
Qui non è possibile visualizzare il rettangoloide (a rigore, dovremmo parlare di rettangoloide generalizzato), giacchè non è possibile tracciare il grafico della funzione in un intorno di x=0. Tuttavia, ripetendo il procedimento di calcolo delle somme integrali, si giunge a una convergenza dell'integrale.

Dagli esempi visti vediamo che nel caso di funzioni con punti di discontinuità di seconda specie nell'intervallo di integrazione [a,b], non sempre le somme integrali risultano convergenti per delta->0, essendo delta la norma di una arbitraria decomposizione di [a,b]. Tale problema fu affrontato e risolto da Riemann per una particolare classe di funzioni, i.e. le funzioni integrabili secondo Riemann. L'integrale di tali particolari funzioni si chiama integrale di Riemann. Successivamente Lebesgue generalizzò ulteriormente l'estensione della nozione di integrale. Ci occuperemo di ciò in un post successivo.