[¯|¯] Funzione di Heaviside, funzione signum

Settembre 17th, 2014 | by extrabyte |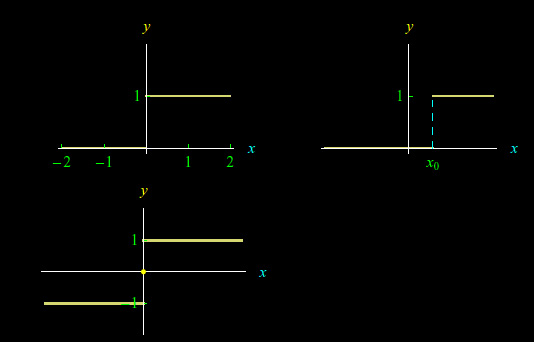

funzione di heaviside,unitstep,funzione signum

Funzione di Heaviside (o gradino unitario o unitstep)

È così definita:

Per definizione di grafico:

Segue

dove:

Cioè il grafico di tale funzione è l'unione della semiretta y=1 di origine (0,1) e del semiasse negativo x privato dell'origine. e si proietta sull'asse x in X=R e sull'asse y in θ(R)={0,1}, come mostrato in figura:

La funzione gradino unitario si generalizza nel seguente modo. Assegnato x₀ in R definiamo:

Il grafico è

essendo

Ne concludiamo che il grafico della funzione unitstep generalizzata è l'unione della semiretta y=1 di origine il punto (x₀,1) e della semiretta y=0 (con x < x ₀) di origine il punto (x₀,0) e privata di tale punto, come illustrato in figura:

Funzione signum

È così definita:

Esplicitando:

Quindi

Da tale equazione possiamo dedurre l'origine del nome dato alla funzione signum, dove "signum" sta per "segno". Infatti, tale funzione agisce alla stregua di un operatore, il quale applicato a un numero reale x restituisce +1 se x > 0, 0, se x=0 e -1 se x < 0. Utilizzando la terminologia informatica, sgnx restituisce gli stati logici +1,0,-1 che definiscono il segno del numero reale x. In altri termini, la funzione signum esegue un'estrazione del segno di un qualunque x preso in R.

Un altro modo di scrivere sgnx consiste nell'utilizzare la notazione di Iverson. Si tratta di una notazione implementata dalle parentesi (di Iverson) definite da una legge di corrispondenza tra l'insieme delle proposizioni associate a un assegnato sistema formale e i valori binari 0,1. Precisamente, sia Π l'insieme delle proposizioni P associate a un sistema formale Σ:

Si osservi che tale legge di corrispondenza è una funzione, per come l'abbiamo definita in una lezione precedente. Risulta:

Pertanto la predetta funzione è definita in Π e il suo codominio è [.](Π)={0,1}. Utilizzando la terminologia informatica, diremo che [P] occupa uno degli stati logici True o False. Ad esempio:

A questo punto possiamo scrivere:

Esaminiamo un ulteriore modalità di scrittura della funzione signum. È facile convincersi che:

Quindi

o ciò che è lo stesso

a patto che x sia diverso da zero.

Per concludere, il grafico della funzione signum è:

dove r₊ è la semiretta y=1 e x > 0 privata dell'origine, mentre r_- è la semiretta y=-1 e x < 0, privata dell'origine. Il grafico è riportato in figura: