[¯|¯] L'integrale di Mengoli-Cauchy e il teorema di Torricelli-Barrow

lunedì, Giugno 1st, 2015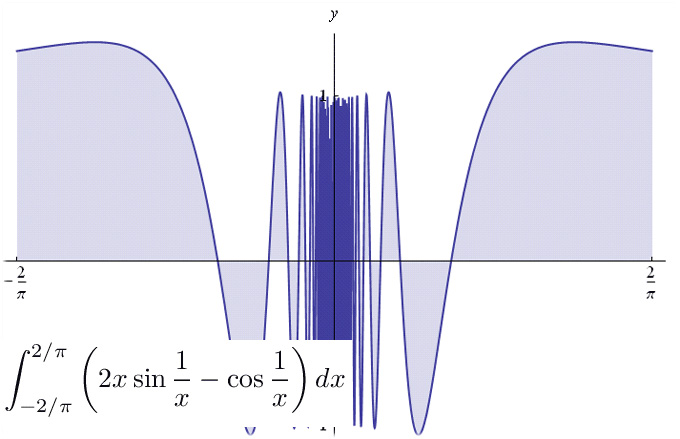

integrale definito, teorema fondamentale del calcolo integrale

In una dispensa precedente abbiamo introdotto la nozione di integrale definito di una funzione continua in un intervallo chiuso e limitato [a,b].
Tale integrale è anche noto in letteratura come l'integrale di Mengoli-Cauchy. Ci si può chiedere se sia possibile estendere tale nozione a funzioni dotate di punti di discontinuità nell'intervallo di integrazione. Nella dispensa di oggi (vedi link più avanti) esaminiamo il comportamento di alcune funzioni non continue in un assegnato intervallo [a,b]. Più precisamente, partiamo dal caso più semplice: funzioni con uno o più punti di discontinuità eliminabili. Ad esempio:

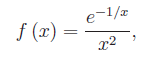
che non è definita in x=0, ma è ivi infinitesima. Quindi ci poniamo il quesito:

discontinuità eliminabili,integrali generalizzati

Calcolando numericamente le somme integrali e facendo tendere a zero l'ampiezza della decomposizione/partizione, si perviene a una risposta affermativa del quesito.
(altro…)