[¯|¯] Funzioni integrabili e funzioni sommabili
venerdì, Febbraio 15th, 2019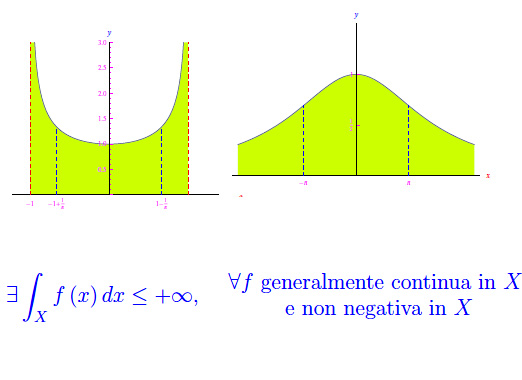
Alcuni esempi numerici esaminati nei numeri precedenti, impongono le seguenti definizioni:
Definizione
Una funzione generalmente continua in un intervallo X (limitato o illimitato) si dice integrabile , se comunque prendiamo una successione di domini {Tn} tali che
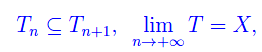
è univocamente determinato il limite:
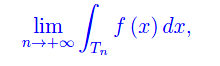
che è l'integrale generalizzato di f esteso all'intervallo X, ossia
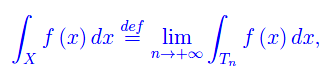
risultando
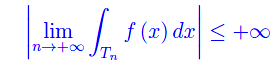
Nota. Nel caso particolare di una funzione non negativa, si ha ovviamente
Nel caso particolare
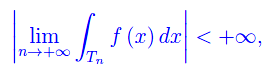
la funzione si dice sommabile.
(altro…)
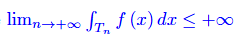
Congettura di Riemann
Trasformata discreta di Fourier
Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier 
Infinitesimi ed infiniti
Limiti notevoli
Punti di discontinuità
Misura di Peano Jordan
Eserciziario sugli integrali
Differenziabilità 
Differenziabilità (2)
Esercizi sui limiti
Appunti sulle derivate
Studio della funzione
Esercizi sugli integrali indefiniti
Algebra lineare
Analisi Matematica 2
Analisi funzionale
Entanglement quantistico
Spazio complesso
Biliardo di Novikov
Intro alla Meccanica quantistica
Entanglement Quantistico
