Riemann era al corrente del lavoro di Chebyschev sui numeri primi

lunedì, Settembre 20th, 2021

numeri primi,riemann,chebyschev
Fig. 1

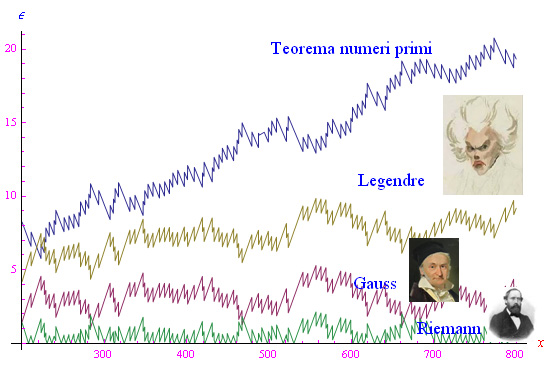
Come è consuetudine, denotiamo con π(x) il numero di numeri primi in [0,x]. Tale funzione è built-in in Mathematica e si denota con PrimePi. Gauss stabilì che la densità dei numeri primi è approssimativamente:


per cui

Costruiamo la seguente tabella:

Nel 1850 Chebyschev dimostrò che nell'approssimazione:

l'errore relativo è non superiore dell'11% per x»1. Più precisamente

(altro…)



Posted in Teoria dei numeri | No Comments »

[¯|¯] Approssimando la distribuzione dei numeri primi

martedì, Luglio 16th, 2019

numeri primi,approssimazione,teorema dei numeri primi,riemann
Fig. 1

Ricordiamo che il valore assunto dalla funzione reale π(x) restituisce il numero di primi in [0,x]. Per il teorema dei numeri primi, il comportamento asintotico di tale funzione è simboleggiato da


Legendre trovò un'approssimazione migliore:


(altro…)



Posted in Teoria dei numeri | No Comments »