Rappresentazione implicita di curve piane (geometria differenziale, meccanica analitica)

lunedì, Novembre 30th, 2020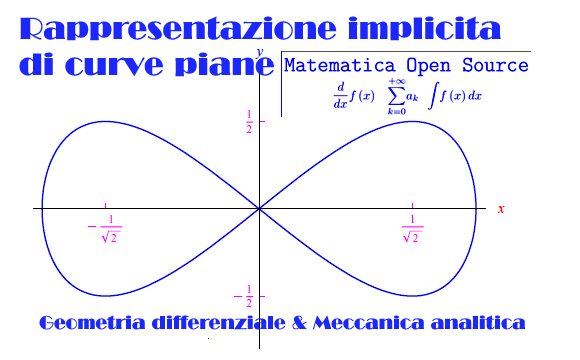

rappresentazione implicita di curve piane,teorema del dini,teorema della funzione implicita

In questo numero consideriamo la rapppresentazionoe implicita di curve piane ossia rappresentate attraverso la nozione di curva di livello di una funzione reale di due variabili reali.

Tale tipo di rappresentazione ci dà comunque la possibilità di passare a una rappresentazione esplicita, almemo localmente, grazie al teorema del Dini (che richiede ovviamente una certa regolarità della funzione F). È dunque cruciale il comportamento del gradiente di F, grazie al quale possiamo classificare e definire i cosiddetti punti singolari di una curva piana. E qui prendiamo i classici due piccioni con una fava 🙂 , nel senso che diamo in maniera molto efficace la nozione di curva regolare (anche se siamo nel caso speciale di una curva piana. Ma il tutto si generalizza facilmente a tre dimensioni).
(altro…)