[¯|¯] Principio dei moti relativi

giovedì, Gennaio 2nd, 2020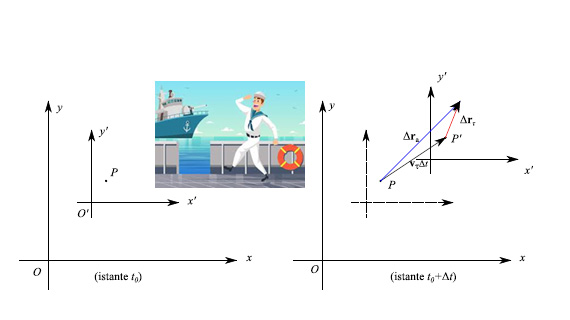

La nozione di sistema di riferimento è vitale per la definizione delle varie grandezze cinematiche (posizione, velocità, accelerazione). A volte si manifesta la necessità di riferire il moto di un punto materiale a due sistemi di riferimento distinti, di cui uno è in movimento rispetto al primo. Sussiste la seguente definizione:
Definizione
Siano K e K' due sistemi di riferimento, di cui K lo possiamo ritenere fisso, mentre K' si muove rispetto a K. Dicesi moto assoluto il moto di un punto materiale rispetto a K. Dicesi moto relativo il moto del medesimo punto rispetto a K'. Il moto di trascinamento è il moto dei punti solidali a K.
Si pensi, ad esempio, ad un marinaio che cammina sul ponte di una nave in navigazione. Schematizzando il marinaio attraverso un punto P ed assumendo come sistema di riferimento fisso un sistema K solidale alla Terra, e come mobile un sistema K' solidale alla nave, il moto assoluto di P è quello del marinaio rispetto alla terraferma, il moto relativo di P è quello del marinaio rispetto alla nave, il moto di trascinamento è quello della nave rispetto alla terraferma.
(altro…)