[¯|¯] Una condizione a cui devono obbedire gli zeri della funzione zeta di Riemann

martedì, Febbraio 13th, 2018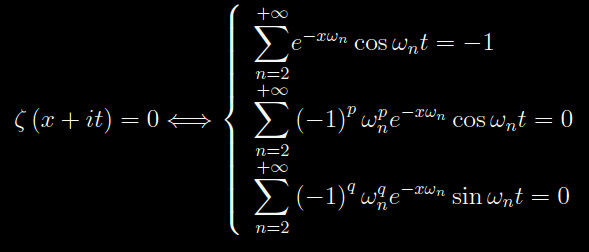

congettura di riemann,zeri non banali,funzione zeta
Fig. 1

Separando parte reale e parte immaginaria della funzione zeta di Riemann e ponendole uguale a zero, si perviene a un sistema di equazioni le cui soluzioni forniscono gli zeri (banali e non banali). Trattandosi di equazioni non esprimibili in forma chiusa, ma attraverso la somma di una serie (uniformemente convergente), non è possibile ottenere una soluzione (che è poi lo scoglio principale per dimostrare la congettura di Riemann). Possiamo comunque eseguire varie manipolazioni algebriche, seguite da una derivazione termine a termine, ottenendo un set di relazioni riportate in fig. 1
(altro…)



Posted in Teoria dei numeri | No Comments »