[¯|¯] Numeri irrazionali e numeri complessi

lunedì, Maggio 21st, 2018

numeri razionali,numeri irrazionali,numeri complessi

Come abbiamo visto in questa lezione, i numeri reali descritti con un numero finito di termini dopo la cifra sono numeri razionali. A questo punto rimane in sospeso la questione se tutti i numeri con infinite cifre significative dopo la virgola siano irrazionali. Dagli esempi già precedentemente introdotti, la risposta è negativa. Gli esempi citati ci dicono che vi sono numeri razionali che hanno un numero infinito di termini dopo la virgola, ma sono periodici. Dimostriamo la seguente asserzione: ogni reale con una parte frazionaria infinita ma periodica è un numero razionale. Per prima cosa torniamo all'esempio esaminato nella lezione precedente, ovvero:

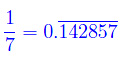
Tale numero si può scrivere come

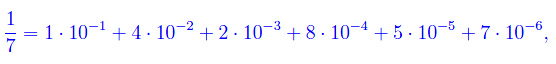
da cui vediamo che il numero si ripete ogni 6 posti, quindi ogni potenza di 10^-6. Definiamo dunque:

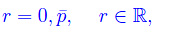
mentre p è un intero della forma:

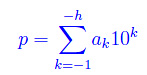
Siccome p è periodico si ripeterà ogni h posti. Ciò implica che possiamo riscrivere r nella seguente forma:

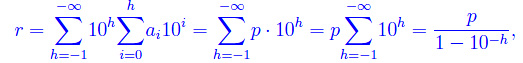
che è manifestamente razionale. (L'ultimo passaggio avviene per via della somma di una serie geometrica di ragione 10^-h).

Dunque si distinguono tre categorie di numeri frazionari: quelli finiti, quelli infiniti ma periodici e quelli infiniti ma non periodici. I primi due tipi provengono da numeri razionali, l'ultima specie da quelli irrazionali. Come si fa a dirlo? Perché siccome i numeri con parte frazionaria finita o periodica sono numeri razionali, non possono venire da numeri irrazionali, che quindi trovano posto solo nei numeri frazionari infiniti non periodici. Tale distinzione, è la base della differenza tra queste due tipologie di numeri.
(altro…)

Posted in Introduzione all'analisi matematica | No Comments »

[¯|¯] Appunti ed esercizi sui numeri complessi

lunedì, Marzo 3rd, 2014

I numeri complessi sono di fondamentale importanza per chi si accinge allo studio dell'analisi matematica (trovano comunque applicazione in altri campi, come ad esempio, in elettrotecnica). Solitamente, i numeri complessi vengono introdotti attraverso l'analisi delle soluzioni dell'equazione algebrica di secondo grado:

x^2 + 1 = 0

Tale equazione è priva di soluzioni nel campo reale. Infatti, non esiste nessun numero reale x tale x^2 = -1. Viene allora eseguita una cosiddetta estensione del campo reale, definendo il campo complesso...

Ecco alcuni link da cui poter scaricare appunti ed esercizi sui numeri complessi: