« Previous Entries

[¯|¯] Quando la differenza ammazza la discontinuità

lunedì, Febbraio 20th, 2017

limiti di funzioni trigonometriche,punti di discontinuità di prima specie, valore assoluto

Fig. 1

Assegnate le funzioni

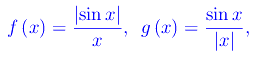
limiti di funzioni trigonometriche,punti di discontinuità di prima specie, valore assoluto

studiare il comportamento di f(x)-g(x) in un intorno di x=0.
Soluzione

Le funzioni f(x) e g(x) hanno in x=0 una discontinuità di prima specie. Se ci limitiamo all'intervallo [-2π,2π] si ha:

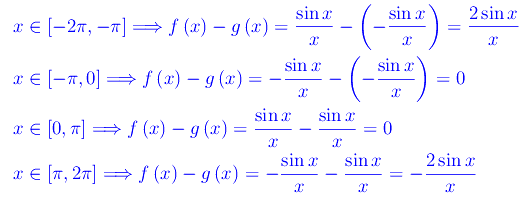
limiti di funzioni trigonometriche,punti di discontinuità di prima specie, valore assoluto

Ne consegue che nel predetto intervallo la funzione f(x)-g(x) è data da:
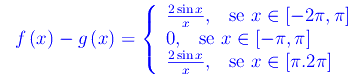
limiti di funzioni trigonometriche,punti di discontinuità di prima specie, valore assoluto

Ciò implica che f(x)-g(x) è continua in x=0
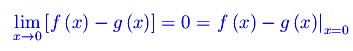
limiti di funzioni trigonometriche,punti di discontinuità di prima specie, valore assoluto

(altro…)



Posted in Analisi Matematica I | No Comments »

[¯|¯] Altra discontinuità di prima specie

lunedì, Febbraio 20th, 2017

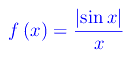
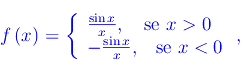
limiti di funzioni trigonometriche,punti di discontinuità di prima specie, valore assoluto

Fig. 1

Classificare i punti di discontinuità della funzione

limiti di funzioni trigonometriche,punti di discontinuità di prima specie, valore assoluto

Soluzione
La funzione è definita in X=R-{0}. Per calcolare i limiti destro e sinistro, esplicitiamo il valore assoluto:

limiti di funzioni trigonometriche,punti di discontinuità di prima specie, valore assoluto

per cui
limiti di funzioni trigonometriche,punti di discontinuità di prima specie, valore assoluto

Ne consegue che x=0 è un punto di discontinuità di prima specie. Il salto di discontinuità è

limiti di funzioni trigonometriche,punti di discontinuità di prima specie, valore assoluto

Il grafico della funzione è riportato in fig. 1.

Indice delle Lezioni










Posted in Analisi Matematica I | No Comments »

« Previous Entries