[¯|¯] Sommabilità di e^-(x)*sin(x)
domenica, Febbraio 17th, 2019
Esercizio
Studiare l'integrabilità della funzione di fig. 1
Soluzione
Osserviamo innanzitutto

Siccome

per il teorema dei carabinieri

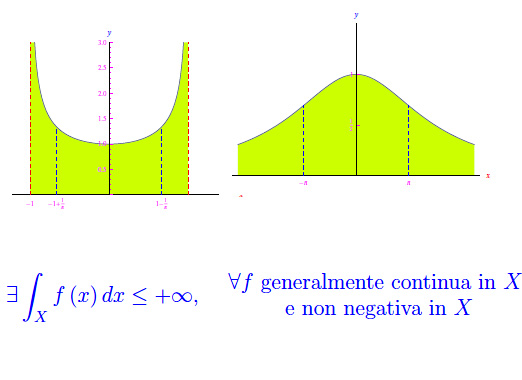
Inoltre, sempre dalla doppia disuguaglianza appena vista, segue che il diagramma cartesiano della funzione

è contenuto nella regione del piano cartesiano

In parole semplici, la funzione oscilla sinusoidalmente tra le curve esponenziali e^(-x) ed -e^(-x), come illustrato in fig. 1. Inoltre, la funzione si annulla infinite volte e i suoi zeri sono:

per cui cambia infinite volte segno. Applicando questo procedimento, si ha:

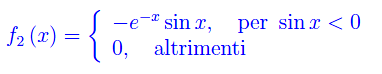
Riesce

essendo R{e-x il rettangoloide generalizzato relativo a e-x di base [0,+oo). Per una nota proprietà della misura segue

Da quest'esempio, si ha

Per la proprietà additiva della misura la precedente si riscrive

Ma

onde

da cui la sommabilità della funzione assegnata. A questo punto possiamo calcolare l'integrale con il solito procedimento di passaggio al limite:

che si calcola facilmente, ottenendo il risultato di fig. 1.

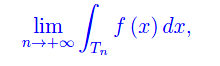
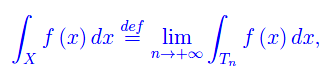
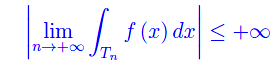
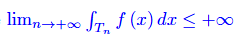
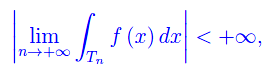


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











