La ricorsività secondo Hofstadter

venerdì, Maggio 28th, 2021

Nel best seller Goedel, Escher, Bach, un'eterna ghirlanda brillante l'autore (Douglas Hofstadter) espone in maniera originale l'importante nozione di ricorsività. Per essere più specifici, a pag. 144 (ed. Adelphi) si parla di "toccare il fondo". Ciò significa assegnare il valore iniziale di una successione ricorsivamente definita. Per fissare le idee sia data la successione:

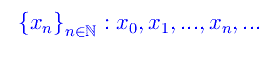
La definizione ricorsiva consiste nell'assegnare una funzione reale f(x) tale che

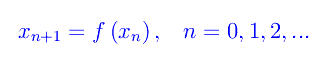
ed è chiaro che la successione è univocamente determinata dal valore iniziale x0. È facile persuadersi che ciò equivale nel continuo ad assegnare un problema di Cauchy relativo a un'equazione differenziale ordinaria del primo ordine autonoma. Più precisamente, definiamo la funzione reale:

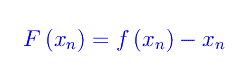
(altro…)

Posted in Libri, Logica Matematica | No Comments »

Strani Anelli e paradossi topologici (bottiglia di Klein)

lunedì, Maggio 24th, 2021

strani anelli, hofstadter,bottiglia di klein

Douglas Hofstadter nel suo best seller Gödel, Escher, Bach: un'eterna ghirlanda brillante introduce la nozione di Strano Anello. In sostanza, si tratta di un processo ciclico che si realizza tra due livelli distinti, in cui il livello per così dire "superiore", viene «riportato» al livello inferiore. Come immagine metaforica, Hofstadter utilizza le famose litografie di Escher come ad esempio, Salita e discesa. Ne segue l'esistenza di una componente autoreferenziale che si propaga un numero infinito di volte. Da qui il termine "Anello", in quanto tale oggetto rappresenta l'infinito attraverso un processo finito (la superficie di un anello è finita, ma può essere percorsa un numero infinito di volte).
(altro…)