[¯|¯] Dirac ha a disposizione infiniti pettini di ordine N
martedì, Febbraio 14th, 2017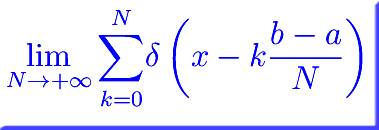
Eseguiamo una decomposizione D([a,b]) di un intervallo [a,b] contenuto nell'insieme R dei numeri reali, ssegnando ad arbitrio N+1 punti, essendo N un intero naturale non nullo.
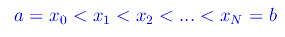
La norma o ampiezza della decomposizione è il numero reale positivo:
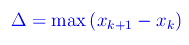
Segue che [a,b] si decompone in N intervalli:
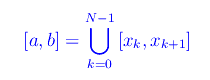
Il numero di punti della decomposizione si esprime formalmente
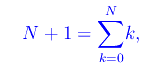
dove δ(x-xk) è la funzione delta di Dirac centrata in xk. Quindi
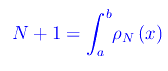
Dal momento che
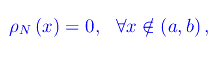
si può scrivere:
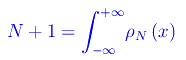
(altro…)
Congettura di Riemann
Trasformata discreta di Fourier
Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier 
Infinitesimi ed infiniti
Limiti notevoli
Punti di discontinuità
Misura di Peano Jordan
Eserciziario sugli integrali
Differenziabilità 
Differenziabilità (2)
Esercizi sui limiti
Appunti sulle derivate
Studio della funzione
Esercizi sugli integrali indefiniti
Algebra lineare
Analisi Matematica 2
Analisi funzionale
Entanglement quantistico
Spazio complesso
Biliardo di Novikov
Intro alla Meccanica quantistica
Entanglement Quantistico
