[¯|¯] Tensori controvarianti (seconda parte)
lunedì, Giugno 5th, 2017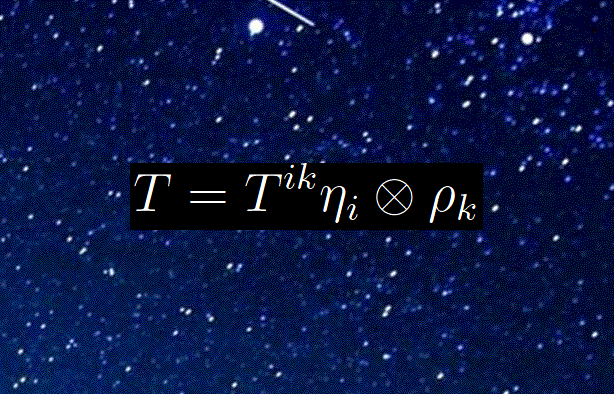
Nel post precedente abbiamo definito i tensori controvarianti di rango 2 quali elementi dello spazio vettoriale dato dal prodotto tensoriale degli spazi vettoriali En e Fm sul medesimo campo K. Per quanto precede, ci aspettiamo che gli elementi di matrice Tik siano le componenti del tensore T in una base del predetto spazio.
Ciò premesso, consideriamo le forme lineari:
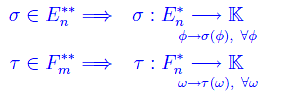
È chiaro che si tratta di vettori controvarianti e a meno di un isomorfismo naturale, si riconducono ad elementi appartenenti a En e Fn rispettivamente. In ogni caso abbiamo:
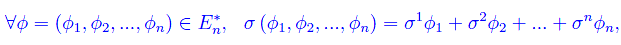
ove σi sono le componenti di σ in una base assegnata di En**. Denotando con {ηi} tale base, si ha:
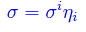
D'altra parte, σi sono anche gli elementi di matrice della forma lineare s nella base duale {θi} associata a {ei}, per cui
(altro…)

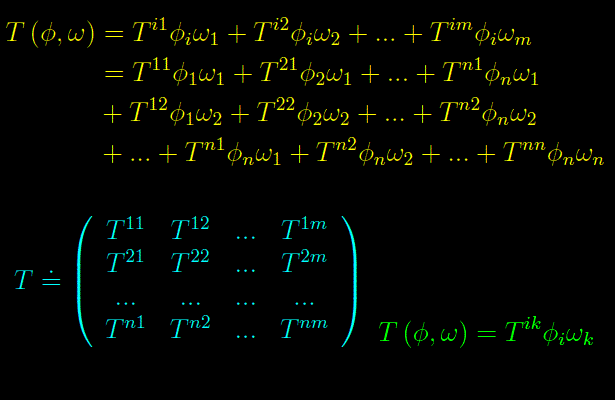
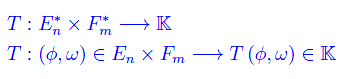
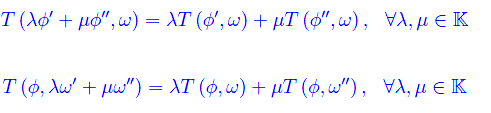
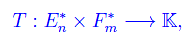


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











