[¯|¯] Regione del piano dove non c'è funzione
giovedì, Febbraio 16th, 2017
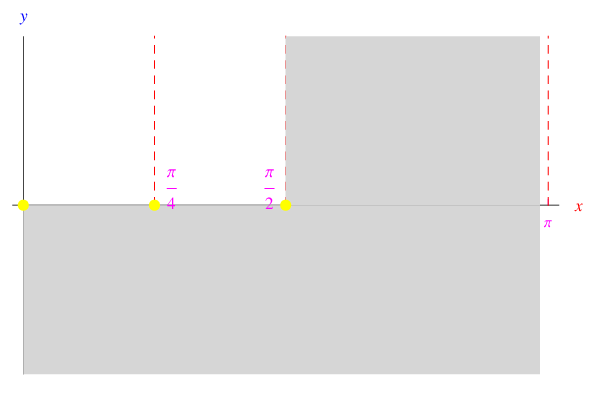
Fig. 1
Esercizio
Classificare i punti di discontinuità della funzione
Soluzione
Dal momento che abbiamo una funzione periodica di periodo T=π riferiamoci all'intervallo [0,π]. Evidentemente
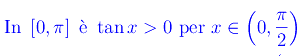
Dobbiamo poi escludere la discontinuità di tan2x nell'intervallo (0,(π/2)). Deve perciò essere:
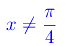
In definitiva il campo di esistenza che ci interessa è
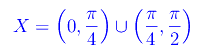
Per quanto riguarda il segno, si ha manifestamente
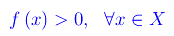
In figura la regione in grigio denota la porzione del piano cartesiano non attraversata dal grafico della funzione, mentre i pallini gialli indica i punti di accumulazione non appartenenti a X.
Studiamo il comportamento della funzione in un intorno destro di x=0. Abbiamo
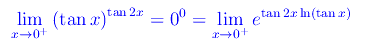
Calcoliamo a parte
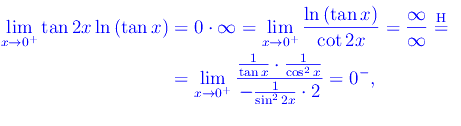
per cui
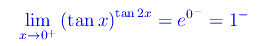
Ne consegue che x=0 è una discontinuità eliminabile. Passiamo al punto x=π/4:
applicando il il procedimento standard
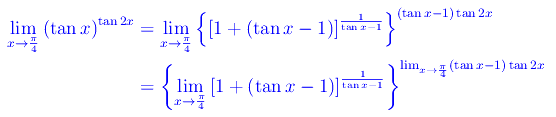
(altro…)
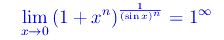
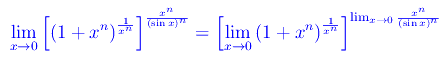
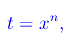
Congettura di Riemann
Trasformata discreta di Fourier
Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier 
Infinitesimi ed infiniti
Limiti notevoli
Punti di discontinuità
Misura di Peano Jordan
Eserciziario sugli integrali
Differenziabilità 
Differenziabilità (2)
Esercizi sui limiti
Appunti sulle derivate
Studio della funzione
Esercizi sugli integrali indefiniti
Algebra lineare
Analisi Matematica 2
Analisi funzionale
Entanglement quantistico
Spazio complesso
Biliardo di Novikov
Intro alla Meccanica quantistica
Entanglement Quantistico
