[¯|¯] Estremi di una funzione reale di una variabile reale
mercoledì, Novembre 26th, 2014
Sia f:X->Y una qualunque funzione reale.
Definizione
f è limitata superiormente se il codominio di f è limitato superiormente. Cioè se:
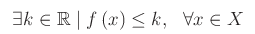
Il numero reale k si dice maggiorante del codominio di f. In maniera analoga diremo che f è limitata inferiormente se il suo codominio è limitato inferiormente. Cioè se:
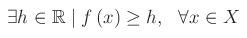
Il numero reale h è un minorante del codominio di f.
Le nozioni di estremo superiore ed estremo inferiore di un insieme (note dal corso di Algebra) si applicano all'insieme numerico X, per cui restano definiti l'estremo superiore e l'estremo inferiore della funzione f che si indicano con i simboli:
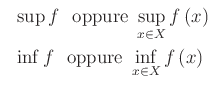
(altro…)
Congettura di Riemann
Trasformata discreta di Fourier
Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier 
Infinitesimi ed infiniti
Limiti notevoli
Punti di discontinuità
Misura di Peano Jordan
Eserciziario sugli integrali
Differenziabilità 
Differenziabilità (2)
Esercizi sui limiti
Appunti sulle derivate
Studio della funzione
Esercizi sugli integrali indefiniti
Algebra lineare
Analisi Matematica 2
Analisi funzionale
Entanglement quantistico
Spazio complesso
Biliardo di Novikov
Intro alla Meccanica quantistica
Entanglement Quantistico
