[¯|¯] Gas ideale di Fermi

giovedì, Febbraio 20th, 2020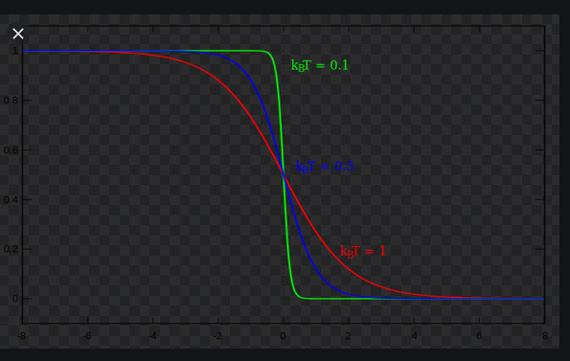

gas di fermi, statistica di fermi dirac,energia di fermi

Definizione
Dicesi gas ideale di Fermi un qualunque sistema costituito da N particelle identiche che seguono la statistica di Fermi-Dirac, confinate in una regione R di volume V.

Il sistema è libero da campi di forza esterni, mentre le pareti del recipiente sono considerate perfettamente riflettenti, cosicché l'energia potenziale di singola particella è

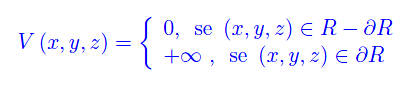
L'hamiltoniana del sistema è

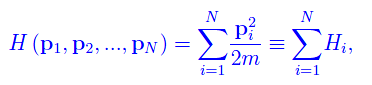
dove

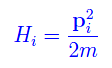
è ovviamente l'hamiltoniana di singola particella, a cui corrisponde quantisticamente un operatore hermitiano. Dal momento che le particelle sono confinate in R, lo spettro degli autovalori è discreto, mentre per V»1 è quasi-continuo. Siccome l'hamiltoniana dell'intero sistema non dipende dalle coordinate di singola particella, si ha che ci stiamo riferendo allo spazio degli impulsi. Quest'ultimo viene suddiviso in cellette ciascuna di volume h³, dove h è la costante di Planck. Quindi lo stato del sistema è determinato univocamente dalla N-pla (p₁,p₂,...,p_N). Scriviamo