Definizione di limite di una funzione reale di una variabile reale (con Mathematica)

giovedì, Febbraio 4th, 2016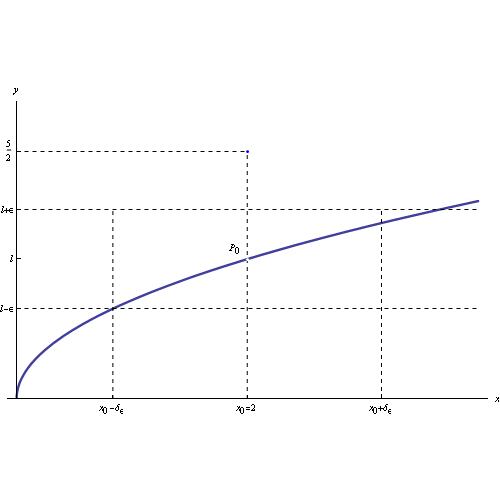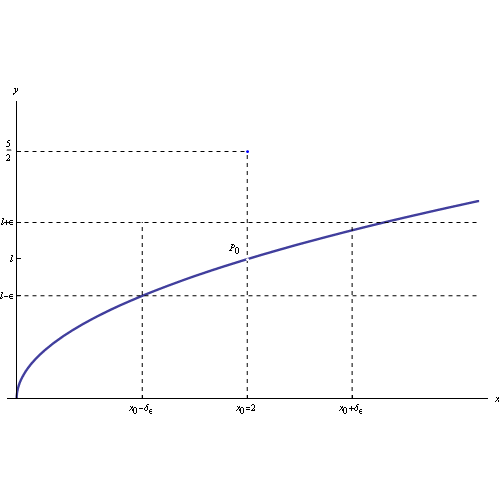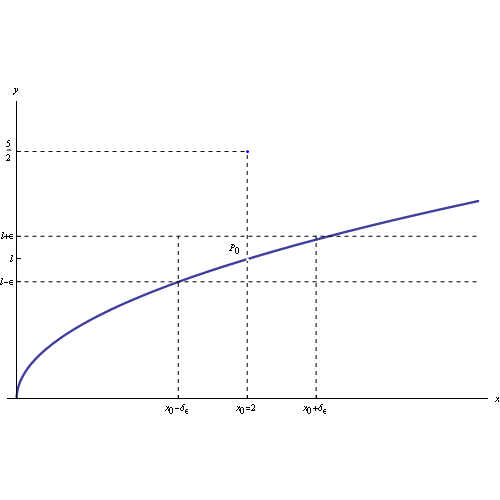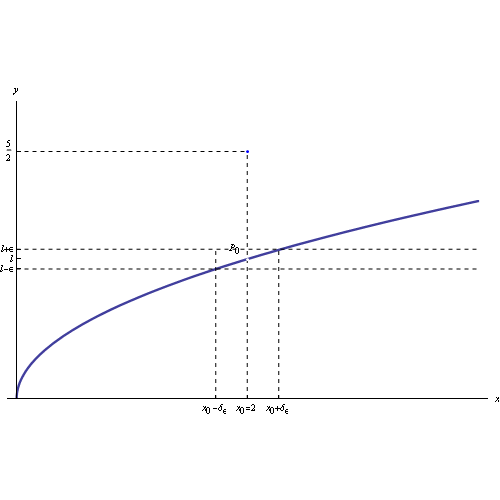

definizione di limite,funzioni,Mathematica

Assegnata una funzione reale di una variabile reale f(x), diremo che tale funzione tende al limite l per x->0, dove x0 è un punto di accumulazione per il campo di esistenza di f, se possiamo rendere arbitrariamente piccola la differenza |f(x)-l|, a patto di prendere x sufficientemente prossimo a x0. Più rigorosamente:

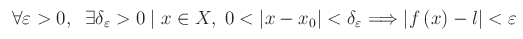
Quindi scriviamo:

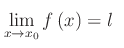
Ad esempio:

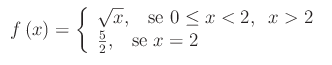
Otteniamo:

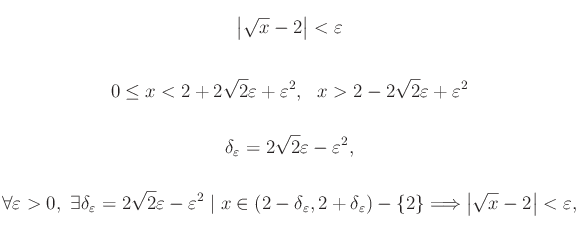
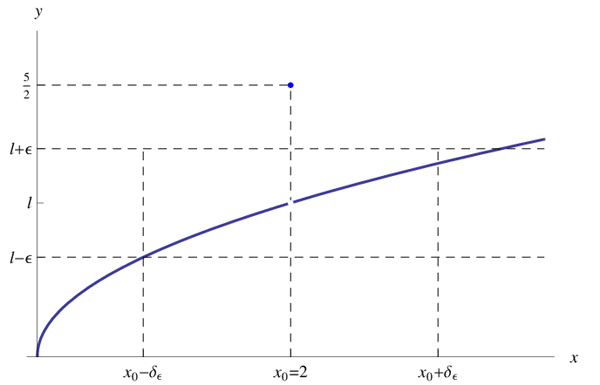
Ne consegue che i punti del grafico della funzione appartenenti al prodotto cartesiano dei predetti intorni, sono contenuti in un rettangolo centrato in P0(x0,l), come illustrato in fig:

Posted in Analisi Matematica I | 1 Comment »

[¯|¯] Definizione di limite (di una funzione reale di una variabile reale)

sabato, Agosto 9th, 2014

Sul sito web di matematica interattiva della Wolfram, la cui URL è demonstrations.wolfram.com/ c'è un interessante definizione interattiva di limite di una funzione reale di una variabile reale.
(altro…)