[¯|¯] Seguendo le orme di Vinogradov e di Korobov (Ipotesi di Riemann)

lunedì, Settembre 2nd, 2019

Il matematico russo Ivan Matveevic Vinogradov, padre della Teoria analitica dei numeri, elaborò un algoritmo di riduzione di complicate somme esponenziali. Tale algoritmo è applicabile alla Congettura di Riemann, come spiegato in questa tesi di laurea. Sembra, tuttavia, che molti risultati interessanti furono ottenuti da un suo studente (Korobov).

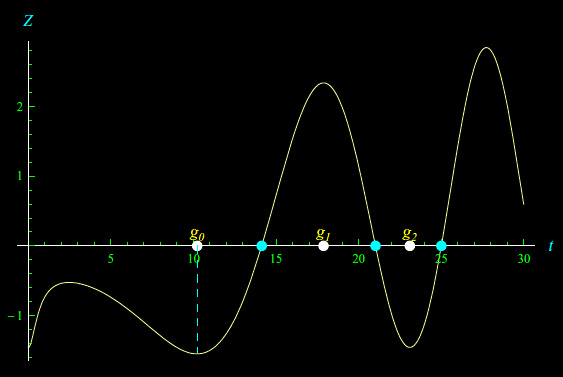
Qualunque sia il metodo di attacco, se si vuole dimostrare per assurdo la congettura di Riemann, è necessario disporre degli adeguati strumenti matematici. Scopo di quest'articolo è, infatti, una possibile definizione di densità degli zeri della funzione zeta di Riemann. Ovviamente tale densità è definita nel senso delle distribuzioni, a causa della natura "discreta" dell'insieme degli zeri non banali appartenenti a un qualunque dominio limitato e misurabile contenuto nella fascia critica.

(altro…)

Posted in Teoria dei numeri | No Comments »

[¯|¯] Mapping di Gram Points e la congettura di Riemann

domenica, Settembre 1st, 2019

In una prima e rozza definizione, i Gram Points sono punti di estremo relativo per la funzione di Riemann-Siegal (nota anche come funzione di Hardy). In realtà, detti punti ci danno info importanti sulla distribuzione degli zeri della predetta funzione lungo la famigerata linea critica relativa alla congettura di Riemann. D'altra parte, il noto fenomeno di Lehmer rende problematica la ricerca dei gram points nell'intervallo considerato, e ciò sembrerebbe contraddire la congettura.
(altro…)