[¯|¯] Alcune osservazioni sulle funzioni sommabili
sabato, Marzo 2nd, 2019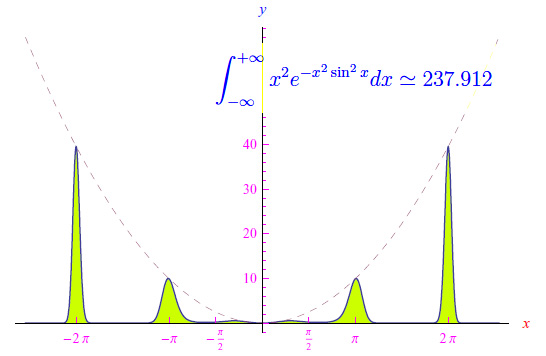
Abbiamo stabilito l'esistenza di una classe di funzioni continue in (-oo,+oo) ed ivi sommabili, pur non annullandosi all'infinito. La più generale funzione della predetta classe è:
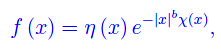
ove b > 0, mentre η(x) se non è una costante è divergente all'infinito. invece, la funzione χ(x) è periodica. Ad esempio:
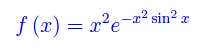
Per quanto stabilito:
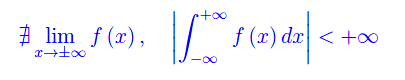
Ciò è una conseguenza del fatto che i criteri di sommabilità esprimono condizioni sufficienti ma non necessarie. Nel caso particolare della sommabilità in un intervallo illimitato, si ha, ad esempio:

Ciò premesso, dimostriamo il teorema:
Teorema
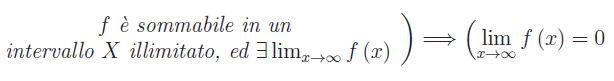
Dim.
Per fissare le idee, supponiamo X=(a,+oo). Procediamo per assurdo, negando la tesi:
dove
(altro…)

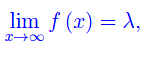
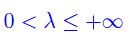


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











