[¯|¯] MAXIMA, un sistema di computer algebra open source

mercoledì, Ottobre 22nd, 2014

maxima,computer algebra system,open source — **Fonte dell'immagine**

MAXIMA un C.A.S. open source.

Cos'è un C.A.S?

C.A.S è l'acronimo di Computer Algebra System, ovvero sistema di computer algebra. Si tratta, dunque, di un software orientato al calcolo simbolico e al calcolo numerico.
(altro…)

Posted in Software | No Comments »

[¯|¯] La funzione parte intera di x

giovedì, Settembre 18th, 2014

funzione parte intera,integerpart — **Fig. 1**

Rammentiamo la definizione di parte intera di un numero reale. Assegnato un qualunque numero reale x, scriviamone la rappresentazione decimale:

dove p è un intero naturale assegnato, mentre c_k appartengono all'insieme {0,1,...,9}.

Poniamo per definizione:
\begin{equation}
\left[ x\right] \overset{def}{=}\pm p
\end{equation}
Cioè denotiamo con $\left[ x\right]$ la parte intera di $x\in \mathbb{R}$ . Ciò premesso, la funzione parte intera di $x$ è:
\begin{equation}
\underset{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\longrightarrow\left[x\right] ,\,\,\,\,\forall x\in\mathbb{R}}{f:\mathbb{R}\rightarrow\mathbb{Z}%},\label{eq: funzione_parte_intera}%
\end{equation}
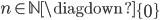
Se $n\in\mathbb{N}\diagdown\left\{ 0\right\}$ , si ha:
\begin{align*}
x & \in\left[ n-1,n\right) \Longrightarrow\left[ x\right] =n-1\\
x & \in\left( -n,-n+1\right] \Longrightarrow\left[ x\right] =-n+1
\end{align*}
Esplicitiamo alcuni valori di $n$ :
\begin{align*}
n & =1\Longrightarrow\left\{
\begin{array}
[c]{l}%
x\in\left[ 0,1\right) \Longrightarrow\left[ x\right] =0\\
x\in\left( -1,0\right] \Longrightarrow\left[ x\right] =0
\end{array}
\right. \\
n & =2\Longrightarrow\left\{
\begin{array}
[c]{l}%
x\in\left[ 1,2\right) \Longrightarrow\left[ x\right] =1\\
x\in\left( -2,-1\right] \Longrightarrow\left[ x\right] =-1
\end{array}
\right. \\
n & =3\Longrightarrow\left\{
\begin{array}
[c]{l}%
x\in\left[ 2,3\right) \Longrightarrow\left[ x\right] =2\\
x\in\left( -3,-2\right] \Longrightarrow\left[ x\right] =-2
\end{array}
\right. \\
& ...,
\end{align*}