» Esercizi svolti di Matematica e Fisica

[¯|¯] Kernel (o nucleo) di un'applicazione lineare

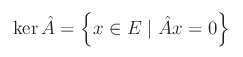
essendo 0 il vettore nullo di F. Si dimostra che kerA è un sottospazio vettoriale di E, la cui dimensione è la nullità di A. Assegnata la base {e₁,...,e_n}} di E e la base {f₁,...,f_m}} di F, dove stiamo supponendo dimE=n,dimF=m, segue che la matrice rappresentativa di A nelle predette basi è:

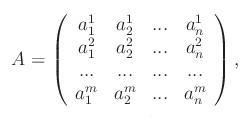
i cui vettori colonna sono le componenti dei vettori quale risultato dell'applicazione di A ai vettori di base di E.
(altro…)

Posted in Algebra Lineare | No Comments »

[¯|¯] Appunti sulle applicazioni lineari

L'autore di queste dispense è il prof. A. Lizzio.

Il download è gratuito. Tuttavia è necessario osservare eventuali limitazioni alla pubblicazione degli appunti e il copyright delle opere (appartiene ai singoli autori).

(altro…)

Posted in Algebra Lineare | No Comments »