» Esercizi svolti di Matematica e Fisica

[¯|¯] Il problema del calcolo computazionale della trasformata di Fourier

venerdì, Giugno 29th, 2018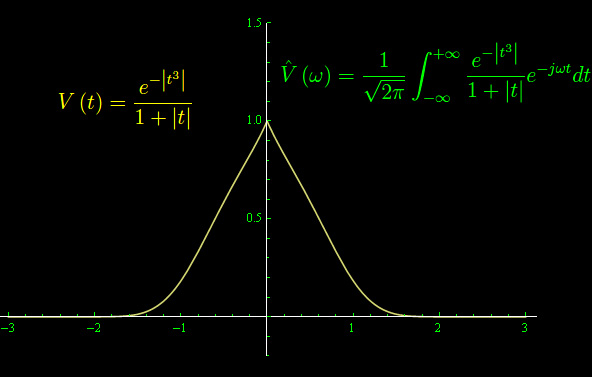

Nel numero precedente abbiamo rinunciato al calcolo dell'espressione analitica della funzione di autocorrelazione, a causa della complessità computazionale del corrispondente integrale. Con Mathematica non è stato possibile calcolare la trasformata di Fourier nemmeno numericamente a causa delle rapide oscillazioni della funzione integranda. Prima di addentrarci nel problema, consideriamo un esempio più semplice:

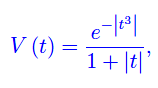
Nel notebook di Mathematica, carichiamo il package per il calcolo numerico della trasformata:

Quindi definiamo la funzione da trasformare, utilizzando l'assegnazione immediata e non quella ritardata, in modo da ridurre il carico computazionale (si noti l'utilizzo del terminatore ; in modo da impedire la visualizzazione dell'output, che avrebbe restituito la funzione in input).

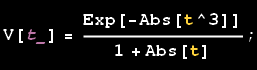
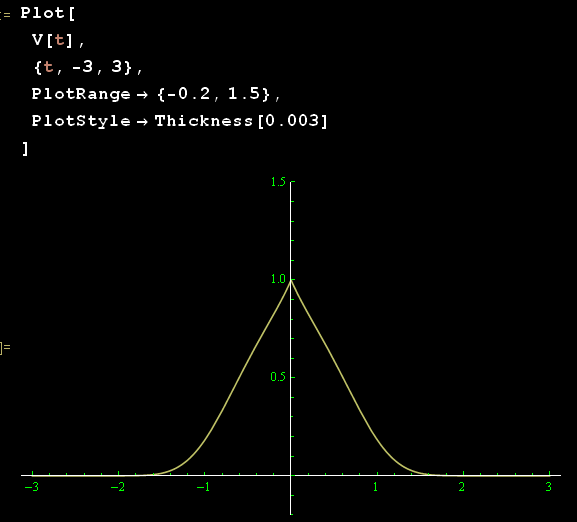
Grafichiamo:

Chiediamo a Mathematica di calcolare la trasformata in modalità simbolica. Il "running" riesce interminabile, per cui lo tronchiamo, provando poi calcolare per via numerica la trasformata per un assegnato valore della variabile ω

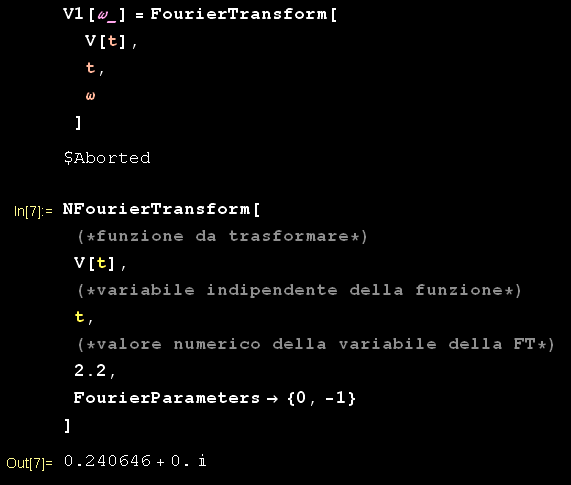
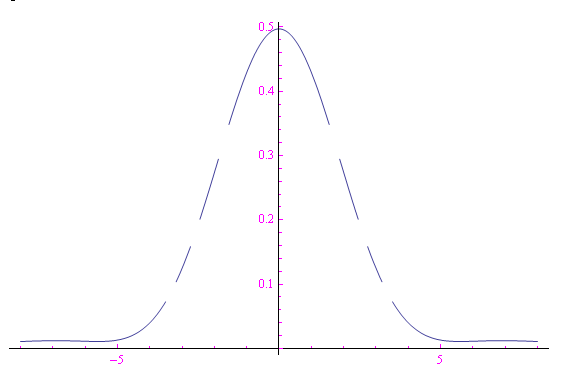
Infine, volendo graficare la trasformata, forziamo l'espressione numerica con la potente istruzione Evaluate:

---

Posted in Elettrotecnica, Mathematica, Software, Teoria dei segnali | No Comments »

[¯|¯] Esperimenti computazionali con il white noise

giovedì, Giugno 21st, 2018

In un post precedente abbiamo visto che la funzione di autocorrelazione di una variabile aleaotoria gaussiana, è una funzione SINC.
In sostanza, la funzione di autocorrelazione ci dice come sono correlati a tempi diversi i valori di una assegnata grandezza (aleatoria o deterministica). È chiaro che se la predetta funzione è identicamente nulla o più precisamente, una funzione delta di Dirac, allora i valori della variabile aleatoria sono scorrelati al 100%. È proprio quello che succede in un white noise. Per verificarlo, utilizziamo Mathematica. Definiamo una funzione random[] che genera numeri reali pseudocasuali:

Generiamo una lista di lunghezza n, di tali numeri:

Utilizziamo l'istruzione ListLinePlot[] per plottare la lista:

(altro…)

---

Posted in Mathematica, Teoria dei segnali | No Comments »