» Esercizi svolti di Matematica e Fisica

[¯|¯] La derivata, ovvero il limite del rapporto incrementale

Ottobre 23rd, 2014 | by extrabyte |

Assegnata una funzione reale di una variabile reale f(x), diremo che tale funzione è derivabile in un punto x₀ del proprio campo di esistenza se e solo se esiste finito il limite del rapporto incrementale:

dove h è l'incremento della variabile indipendente. Per quanto detto, se il rapporto incrementale inteso come funzione della variabile reale h è convergente per h->0, cioè se il limite:

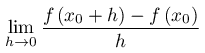
esiste finito, allora diremo che la funzione è derivabile in x₀ e chiamiamo tale limite la derivata di f(x) nel punto x₀.

Utilizzando la notazione apicale di Lagrange, scriviamo:

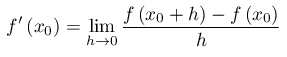
Mentre con la notazione di Leibnitz:

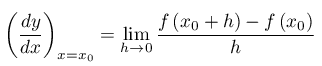
La funzione si dirà poi derivabile nel proprio campo di esistenza X, se è derivabile in ogni punto di X.

Applicando la definizione di derivata è possibile determinare la derivata delle funzioni elementari. Nell'animazione grafica seguente

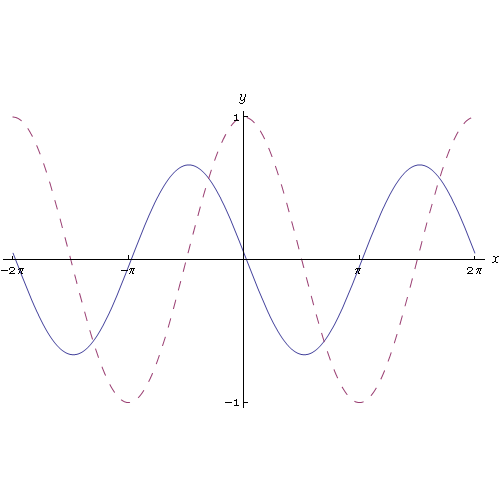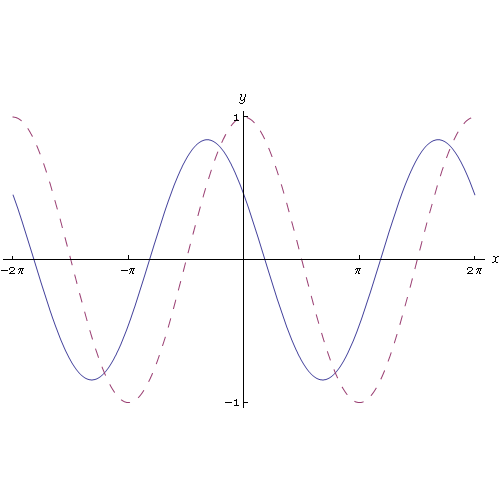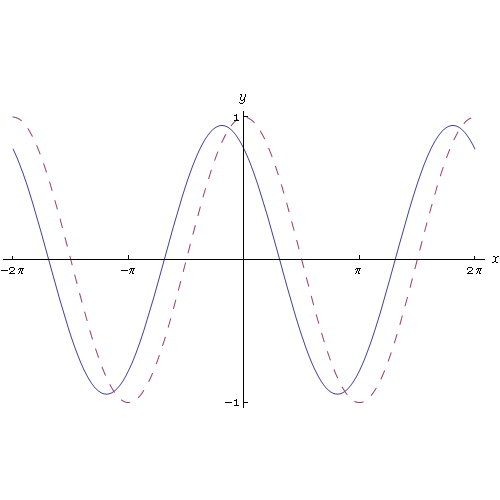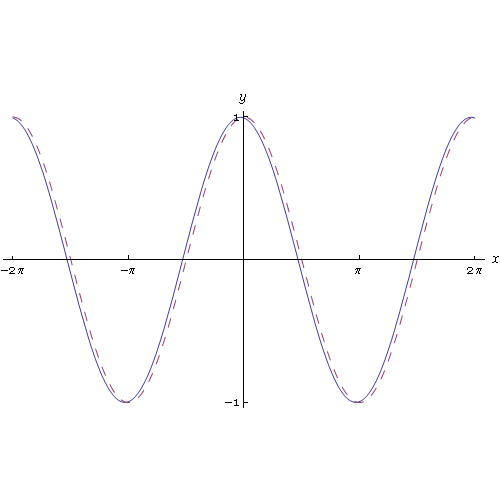
vediamo una interessante approssimazione del rapporto incrementale relativo alla funzione sin(x), la cui derivata è la funzione cos(x). Al tendere a zero dell'incremento h vediamo che il rapporto incrementale tende al cos(x).

Tags: Definizione di derivata di una funzione reale di variab, Limite del rapporto incrementale, notazione apicale di Lagrange, Notazione di Leibnitz, Rapporto incrementale

Articoli correlati