Dalla disuguaglianza di Schwartz alla relazione di indeterminazione
Dicembre 28th, 2022 | by Marcello Colozzo |
Algebra dei ket

dove f,g sono continue in [a,b], nota come disuguaglianza di Schwarz. In realtà, questo è un caso particolare giacché stiamo considerando funzioni da [a,b] a R. Più in generale, denotiamo con C°([a,b]) l'insieme delle funzioni continue in [a,b] e a valori in C. Come è noto, tale insieme può essere strutturato come spazio vettoriale sul campo complesso. Introducendo poi il prodotto scalare

il predetto spazio assume la struttura di spazio di Hilbert. E quindi la nozione di norma:

In tale formalismo la disuguaglianza di Schwartz assume la forma più compatta:

valida ovviamente anche nel campo reale (qui abbiamo uno spazio euclideo (infinito dimensionale) anziché uno spazio di Hilbert).
Passiamo ora all'algebra dei ket

essendo

Per dimostrare la disuguaglianza di Schwartz, costruiamo una arbitraria combinazione lineare:

Segue

In virtù dell'arbitrarietà di λ
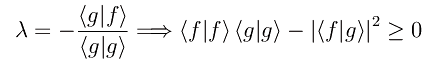
cioè l'asserto.
Ciò premesso, consideriamo una osservabile quantistica A relativa a un assegnato sistema quantistico rappresentato da uno spazio di Hilbert H. A sua volta tale osservabile sarà rappresentata da un operatore hermitiano che indichiamo con lo stesso simbolo. Il valore di aspettazione di A in un generico stato quantistico |ψ> di H è

Definiamo l'operatore hermitiano
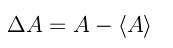
Quindi calcoliamo il valore di aspettazione
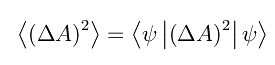
noto come dispersione dell'osservabile A nel predetto stato. Sviluppando il quadrato e dopo semplici calcoli:
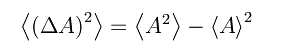
Lemma
Il valore di aspettazione di un operatore hermitiano è puramente reale. Il valore di aspettazione di un operatore anti-hermitiano è puramente immaginario.
Dim.
Siano A e C due operatori, il primo hermitiano e l'altro anti-hermitiano. Rammentiamo la definizione di operatore aggiunto:
Se A è hermitiano:
Segue
Se C è anti-hermitiano:
Terema (i>Relazione di indeterminazione)
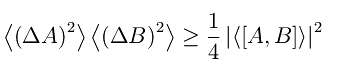
dove [A,B] è il commutatore:
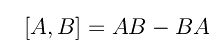
Dim.
Definiamo i ket
Tenendo conto del carattere hermitiano degli operatori ΔA,ΔB, i bra duali sono:
Segue
dove nell'ultimo passaggio abbiamo tenuto conto della disuguaglianza di Schwarz. Dunque
Il prodotto a secondo membro si decompone:
essendo
l'anticommutatore. È facile convincersi che il commutatore è un operatore anti-hermitiano, mentre l'anticommutatore è hermitiano. Quindi per il lemma precedente:
Segue
da cui l'asserto.

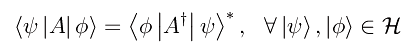
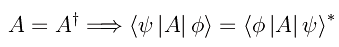
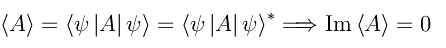
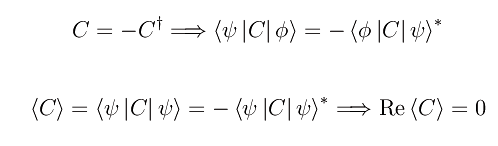
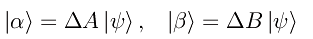
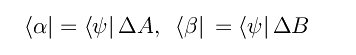
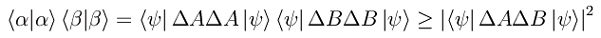
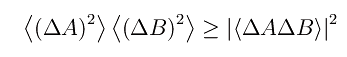
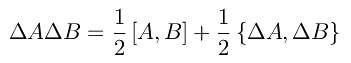
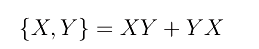
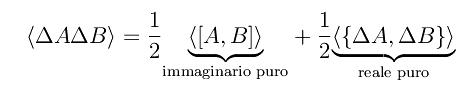
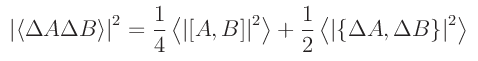


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











