» Esercizi svolti di Matematica e Fisica

L'equazione del covid 19

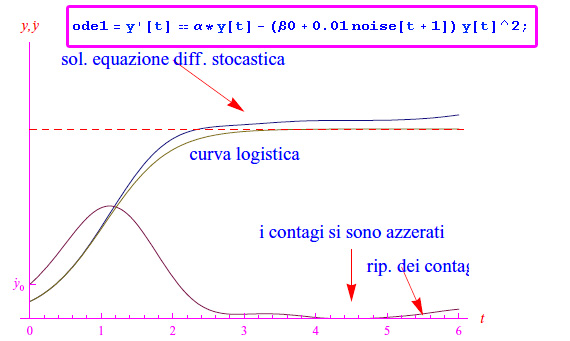
Necessariamente è un'equazione differenziale stocastica. Tale circostanza distrugge la possibilità di implementare modelli in grado di eseguire previsioni affidabili (se non certe).

Ma già se partiamo dall'approssimazione più rozza, i.e. curva pandemica logistica (integrale dell'equazione di Bernoulli), troviamo oo² modelli possibili, giacchè è 2 il numero di parametri liberi (che andrabbero misurati statisticamente). Migliorando il tito, si aggiunge un noise di background che modula il parametro di contenimento. "Giocando" con Mathematica, esce fuori l'andamento di fig. 1.

Tags: covid-19, equazione del covid, equazione differenziale stocastica