Il tasso di contagio R(t) è formalmente l'analogo della costante di Hubble degli Universi di Friedmann

Giugno 1st, 2020 | by Marcello Colozzo |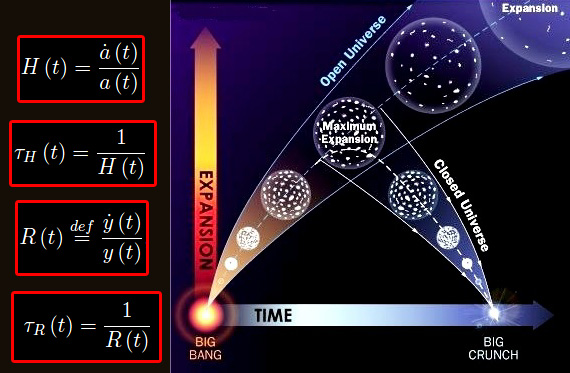

covid,Rt,R0,modelli di friedmann,costante di hubble

Le considerazioni seguenti costituiscono un'analogia formale tra le grandezze R0 e Rt che spesso vengono citate a sproposito. In rete ci sono molte risorse che forniscono una spiegazione a livello statistico delle predette variabili. Tuttavia, un'interpretazione interessante è fornita direttamente dalle equazioni differenziali, che permettono la definizione di una costante di tempo che determina univocamente la scala dei tempi del processo in esame. Il termine "costante" non va preso alla lettera in quanto (in generale) si tratta di funzioni del tempo.

Ricordiamo che in Cosmologia le famose equazioni di Friedmann restituiscono la possibilità di definire una costante di Hubble attraverso il rapporto tra la derivata prima del parametro di espansione della metrica di Robertson-Walker e il parametro medesimo. Ciò suggerisce una analogia con la grandezza R(t). Ci si potrebbe spingere ulteriormente in tale analogia, osservando che nel caso dell'espansione dell'universo, è fondamentale confrontare la scala dei tempi dei processi termodinamici con il tempo caratteristico di espansione. Più precisamente, il raggiungimento dell'equilibrio termodinamico è possibile solo se tali processi sono istantanei nella scala dei tempi di espansione dell'universo.

Scarica il file in pdf

No TweetBacks yet. (Be the first to Tweet this post)