Diffusione virale di background

Aprile 16th, 2020 | by Marcello Colozzo |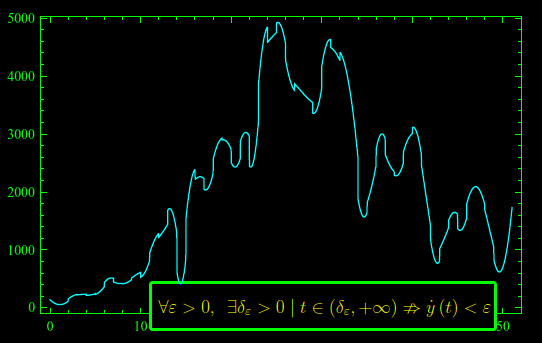

coronavirus,attualmente positivi,processo di wiener,picco massimo — **Fig. 1**

Se y(t) è la funzione caratteristica del processo di diffusione virale (numero di attualmente positivi), affinché il processo venga saturato, deve essere:

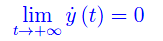
ove la notazione puntata denota la derivata rispetto al tempo. Tuttavia, dall'esame della derivata prima ottenuta per interpolazione in ambiente Mathematica (fig. 1) si deduce un comportamento oscillante (potrebbe addirittura trattarsi di un processo di Wiener, per cui

Non abbiamo inserito il valore assoluto, poiché la predetta derivata è definitivamente non negativa intorno a +oo. In altri termini, la derivata prima non è arbitrariamente piccola intorno a +oo. Ciò implica l'esistenza di un processo virale di background che sotto condizioni favorevoli, potrebbe dar luogo a una nuova pandemia.

No TweetBacks yet. (Be the first to Tweet this post)