» Esercizi svolti di Matematica e Fisica

Infezione da covid-19 e random walk

Aprile 5th, 2020 | by Marcello Colozzo |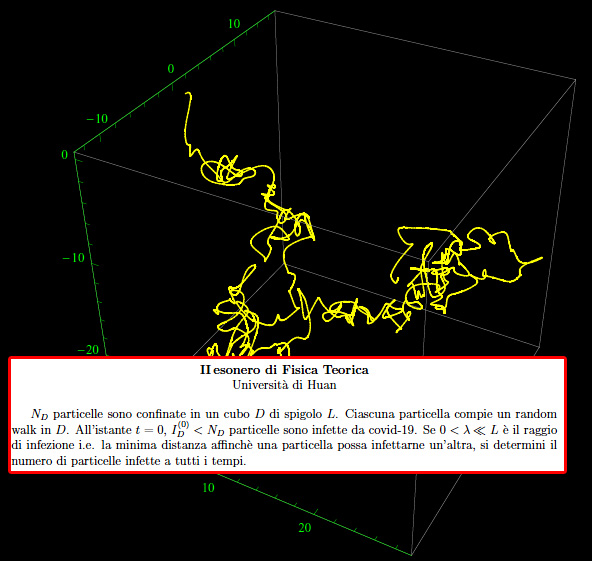

Impostazione
Scriviamo

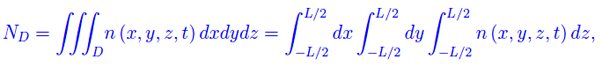
dove n(x,y,z,t) è la densità del numero di particelle nell'istante t. All'istante iniziale:

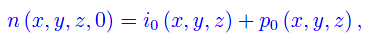
dove i₀(x,y,z) è la densità iniziale di particelle infette, mentre p0(x,y,z) è la densità iniziale di particelle non infette. Deve essere

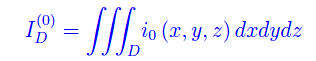
Inoltre

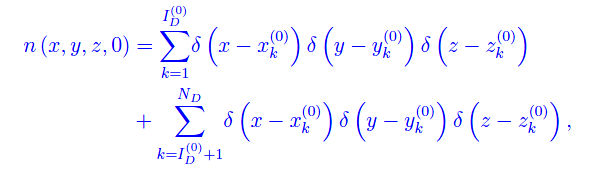
essendo

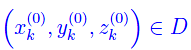
la posizione iniziale di singola particella, mentre δ è la funzione delta di Dirac. Al tempo t:

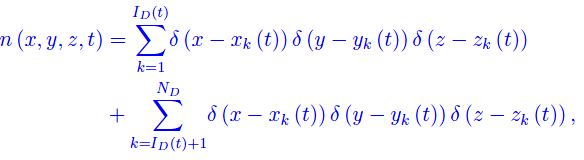
dove x_k(t),y_k(t),z_k(t) definiscono un random walk, come illustrato in fig. 1.









Una condizione sufficiente (ma non necessaria) affinché l'evoluzione dinamica del sistema conservi il numero iniziale di infetti, è

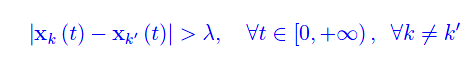
dove x(t)_k è il vettore posizione della k-esima particella. Tale condizione equivale a implementare un random walk di N_D sfere di raggio λ che non entrano mai in collisione.

Tags: covid-19, pandemia, random walk

Articoli correlati