Raggiungimento del picco massimo (asintoto)

Marzo 25th, 2020 | by Marcello Colozzo |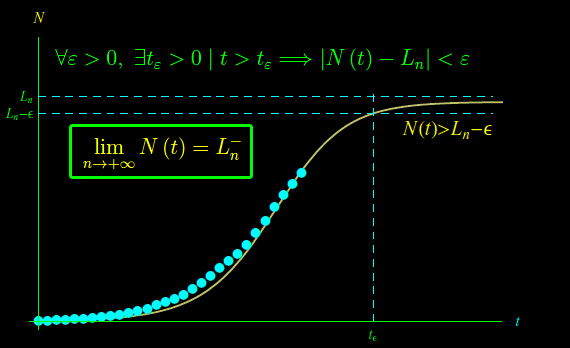

coronavirus,logistica,picco massimo,asintoto — **Fig. 1**

Per quanto precede, abbiamo il seguente comportamento asintotico:

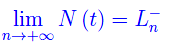
dove l'apice (-) ci dice che N(t) tende a L_n per valori minori di L_n. Impropriamente, il numero reale L_n viene denominato picco massimo. Ma per quanto precede, tale valore viene raggiunto dopo un tempo infinito. D'altro canto, applicando la definizione di limite:

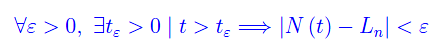
Cioè

Geometricamente significa che per t > t_ε il grafico della funzione N(t) è contenuto nella semistriscia del piano cartesiano (t,N):

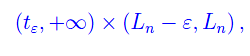
come illustrato in fig. 1. Per continuità ci aspettiamo che

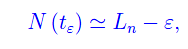
per cui

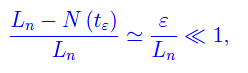
dove l'ultima disuguaglianza è una conseguenza dell'ordine di grandezza di L_n. Precisamente

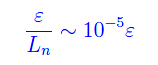
Quindi prendendo un ε sufficientemente piccolo (in base all'ordine di approssimazione desiderato), è possibile determinare (per via numerica) dall'equazione scritta più sopra l'istante t_ε che può essere assunto come istante di picco. Per concludere, osserviamo che nella fig. 1 il valore di ε è "esageratamente grande", in modo visualizzare il comportamento asintotico della funzione N(t).

No TweetBacks yet. (Be the first to Tweet this post)