[¯|¯] Gas ideale di Fermi

Febbraio 20th, 2020 | by Marcello Colozzo |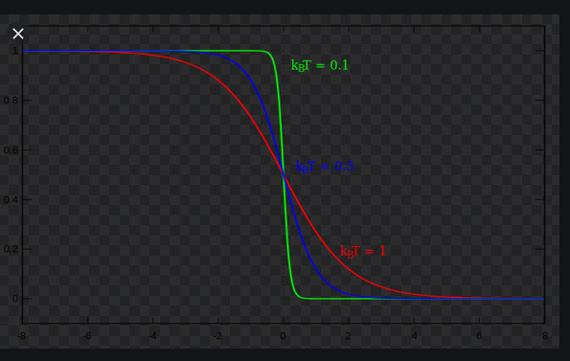

gas di fermi, statistica di fermi dirac,energia di fermi

Definizione
Dicesi gas ideale di Fermi un qualunque sistema costituito da N particelle identiche che seguono la statistica di Fermi-Dirac, confinate in una regione R di volume V.

Il sistema è libero da campi di forza esterni, mentre le pareti del recipiente sono considerate perfettamente riflettenti, cosicché l'energia potenziale di singola particella è

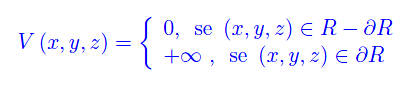
L'hamiltoniana del sistema è

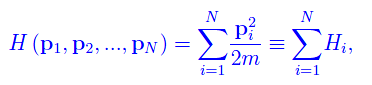
dove

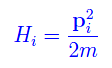
è ovviamente l'hamiltoniana di singola particella, a cui corrisponde quantisticamente un operatore hermitiano. Dal momento che le particelle sono confinate in R, lo spettro degli autovalori è discreto, mentre per V»1 è quasi-continuo. Siccome l'hamiltoniana dell'intero sistema non dipende dalle coordinate di singola particella, si ha che ci stiamo riferendo allo spazio degli impulsi. Quest'ultimo viene suddiviso in cellette ciascuna di volume h³, dove h è la costante di Planck. Quindi lo stato del sistema è determinato univocamente dalla N-pla (p₁,p₂,...,p_N). Scriviamo

Le particelle seguono la statistica di Fermi-Dirac:

ove l'apice ci ricorda che non stiamo considerando il peso statistico dovuto allo spin s, cioè g_s=2s+1:

L'ultimo passaggio si giustifica osservando che stiamo considerando particelle di spin 1/2. La condizione di normalizzazione è

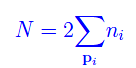
Qui abbiamo ridefinito n_i=0,1. Alla temperatura dello zero assoluto:

Dal momento che in ogni stato possiamo trovare non più di 2 particelle (con spin opposti), alla temperatura dello zero assoluto le particelle si dispongono in stati con impulso crescente da p=0 fino a un massimo p_max=p_F, noto come impulso di Fermi. In approssimazione di spettro continuo:

L'integrale si calcola facilmente passando alle coordinate sferiche nello spazio degli impulsi di singola particella:

Cioè

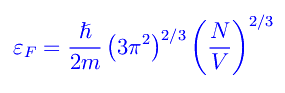
Stiamo considerando un sistema non relativistico, per cui l'energia di singola particella è

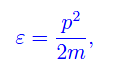
che ci permette di definire l'energia di Fermi:

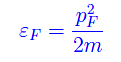
Cioè

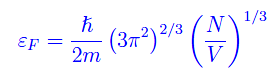
ed una temperatura di Fermi:

Notiamo quindi, che se la temperatura di equilibrio termodinamico del gas è T»T_F, l'energia di Fermi è trascurabilmente piccola nella scala dell'energia del sistema, per cui è come se le particelle occupassero lo stato fondamentale (di energia nulla, dato che non ci sono campi esterni). In altre parole, il gas si comporta seguendo la meccanica statistica classica. Viceversa, se T«T_F, allora l'energia di Fermi non è più trascurabile, e abbiamo una deviazione dal comportamento classico. Tale deviazione è denominata degenerazione.

No TweetBacks yet. (Be the first to Tweet this post)