[¯|¯] Il modello di Thomas-Fermi (parte 1)

Febbraio 15th, 2020 | by Marcello Colozzo |

modello di thomas fermmi, atomo pesante,metodo di hartree-fock,equazione di schrödinger

Come è noto, i livelli energetici di un atomo, quale sistema quantistico non relativistico costituito da Z >= 1 elettroni, costituiscono la soluzione di un problema agli autovalori che in generale, si esprime come

dove: H è l'operatore hamiltoniano del sistema; u_n,E_n sono rispettivamente le autofunzioni e agli autovalori dell'energia; il pedice n denota un set di numeri quantici.

L'equazione appena scritta è la forma operatoriale dell'equazione differenziale di Schrödinger non dipendente dal tempo, che può essere integrata in forma chiusa solo nel caso Z=1 (atomo di idrogeno). Per Z > 1 si ricorre a metodi approssimati, come ad esempio, il metodo autoconsistente di Hartree-Fock. Sfortunatamente, nel caso degli atomi pesanti (Z»1) il predetto metodo esibisce un notevole peso computazionale, per cui viene utilizzato il metodo di Thomas - Fermi. Si tratta di un approccio il cui passo iniziale è dato dalla seguente considerazione:

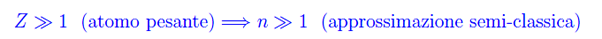
giacché nel limite dei grandi numeri quantici, un qualunque sistema quantistico si comporta quasi classicamente. Inoltre, dalla meccanica statistica quantistica, sappiamo che la massima energia di un sistema di elettroni liberi è nello stato fondamentale del sistema medesimo, pari alla cosiddetta energia di Fermi:

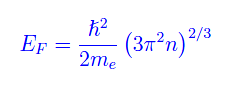
dove non dobbiamo confondere n con il set di numeri quantici precedentemente introdotto. Qui n è la densità del numero di elettroni del sistema, ed è manifestamente una funzione del posto, per cui anche l'energia di Fermi dipende dalle coordinate del punto considerato. Nella formula abbiamo la consueta costante di Planck ridotta, oltre alla massa dell'elettrone.

Ciò premesso, istituendo un sistema di coordinate sferiche (r,θ,&phi) nel "centro" dell'atomo e assumendo una simmetria sferica del campo elettrostatico prodotto dalla carica nucleare +Ze e dagli elettroni -Ze, il problema che si apre consiste nel determinare il potenziale ?(r) del predetto campo. Abbiamo detto che il sistema è quasi in regime classico, per cui l'energia meccanica di singolo elettrone si scrive:

Continua in pdf

No TweetBacks yet. (Be the first to Tweet this post)