» Esercizi svolti di Matematica e Fisica

[¯|¯] Non-integrabilità della funzione SINC

Febbraio 18th, 2019 | by Marcello Colozzo |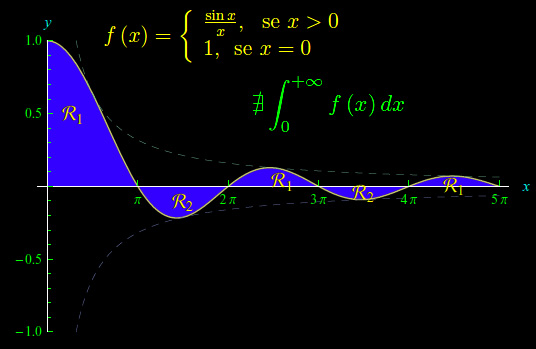

Esercizio
Discutere l'integrabilità in [0,+oo) della funzione di fig. 1

---

Soluzione
Tale funzione è manifestamente continua ed è graficata in fig. 1, essendo

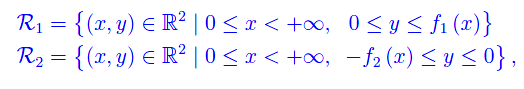
dove

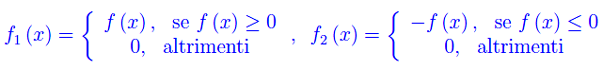
Per essere più specifici, definiamo

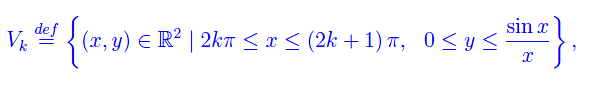
con k=0,1,...,N-1, essendo N un intero positivo preso ad arbitrio. Riesce:










Definiamo

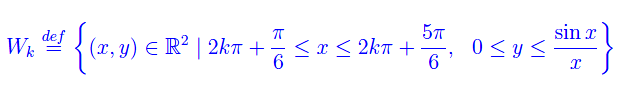
Se ci aiutiamo con il seguente grafico:

vediamo che

Ne consegue

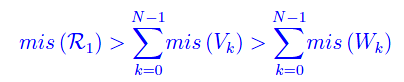
A questo punto osserviamo che

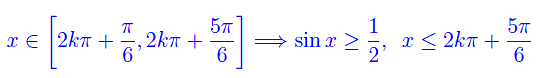
Manipoliamo l'ultimo termine:

per cui

Quindi

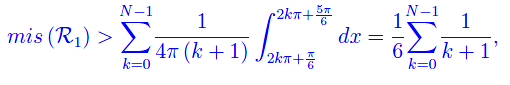
cioè

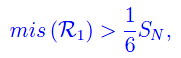
dove

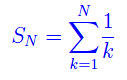
ovvero la somma parziale di ordine N della serie armonica. Come è noto, tale serie diverge

Quindi

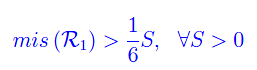
il che equivale a scrivere

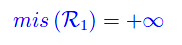
Applicando un procedimento simile a R₂, si perviene a

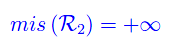
Per quanto stabilito in questa lezione, ne concludiamo che la funzione assegnata è non-integrabile in [0,+oo).

Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

Tags: funzione sinc, non integrabilità

Articoli correlati