[¯|¯] Una massa M scivolando su un piano inclinato trascina una massa m
Novembre 15th, 2018 | by Marcello Colozzo |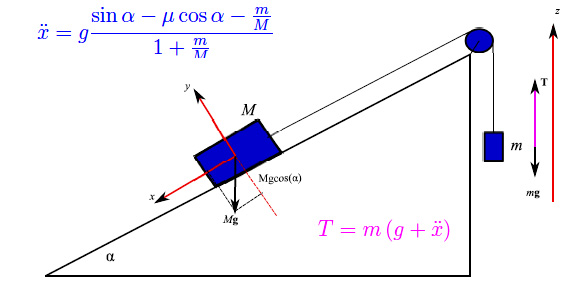
Esercizio
Lungo un piano inclinato di α sull'orizzontale può scendere strisciando un corpo di massa M che, attraverso un filo inestensibile e di massa nulla, provoca la risalita di una massa m. Supponendo di poter trascurare le perturbazioni indotte dalla puleggia su cui scorre il filo e della resistenza dell'aria, si calcoli l'accelerazione della massa M sapendo che il coefficienti di attrito dinamico con il piano è µ. Determinare, poi, la tensione del filo. Infine, supponendo di poter variare l'angolo di inclinazione, per quale valore di α il sistema è in equilibrio (ammettendo che sia inizialmente fermo)?
Dati: M=10kg ,m=1kg ,α=45°,µ=0.5.
Soluzione
Adottiamo un sistema di assi cartesiani ortogonali Oxy come in fig. 1. Su M agiscono le forze:
- P=mg (forza peso)
- RN (reazione normale del vincolo).
- RT(reazione tangenziale del vincolo (attrito)).
- T (tensione del filo).
Se i e j sono i versori degli assi coordinati:

Per il secondo principio della dinamica:

Proiettando tale equazione vettoriale sugli assi coordinati otteniamo il sistema di equazioni scalari:
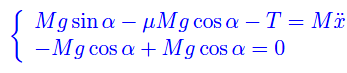
La seconda si riduce all'identità 0=0, per cui consideriamo solo la prima che qui riscriviamo:
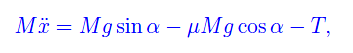
in cui figurano le incognite x e T. Per ottenere una seconda equazione che lega le predette incognite, applichiamo il secondo principio della dinamica alla massa m. A tale scopo orientiamo un asse verticale z come mostrato in fig. 1. Risulta:

essendo k il versore dell'asse z. Proiettando tale equazione sull'asse z:
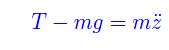
Segue manifestamente:

In altri termini, l'inestensibilità del filo implica che le due masse si muovono con la stessa accelerazione. Ovviamente si tratta di due vettori diversi, ed è solo il modulo che coincide. Diversamente, l'allungamento o l'accorciamento del filo determina accelerazioni diverse. In tale ipotesi otteniamo il sistema di equazioni scalari:

Dalla seconda ricaviamo la tensione del filo:
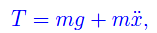
che sostituita nella prima porge:
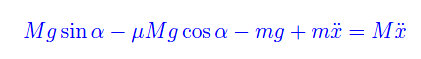
onde

Ed è questa l'accelerazione con cui si muovono le due masse.
Per rispondere al secondo quesito utilizziamo l'equazione della tensione ricavata in precedenza:
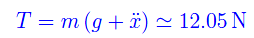
Passiamo al terzo quesito. Deve essere:

Cioè

Tale equazione trigonometrica non si può risolvere analiticamente. Procedendo numericamente o per via grafica, si ottiene:
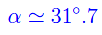
Ne concludiamo che per un angolo di inclinazione 31°.7, le due masse rimangono in equilibrio.
Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.
Tags: accelerazione, attrito, carrucola, filo inestensibile, piano inclinato
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











