» Esercizi svolti di Matematica e Fisica

[¯|¯] I giganti e la lunghezza d'onda di Jeans

Ottobre 24th, 2018 | by Marcello Colozzo |

Siano A e B due persone che conversano ad alta voce. Quando uno dei due parla (ad es., A) le corde vocali generano una fluttuazione di densità dell'aria che si propaga con una data velocità (che è ovviamente la velocità del suono). Per poter modellizzare tale processo fisico, schematizziamo l'aria attraverso un fluido omogeneo ed isotropo. In particolare, supponiamo che la sua densità sia costante e pari a ρ₀. Assumiamo per semplicità, che una fluttuazione di densità δρ generata dalle corde vocali di A sia definita in un dominio sferico di raggio λ. Se Fsub>g è la forza (per unità di massa) dovuta alla gravità, si ha:

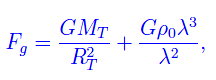
ove il primo termine si riferisce al peso della sfera di aria, mentre il secondo tiene conto dell'autogravitazione. Ritenendo quest'ultimo dominante, riesce

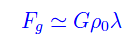
Sulla sfera di raggio λ agisce oltre alla predetta forza dovuta alla gravità, la forza di pressione che riferita all'unità di massa, si scrive:

essendo v_{s} la velocità del suono nel fluido di densità ρ₀.

Condizione di propagazione

Tenendo conto delle espressioni delle forze coinvolte:

dove

è la massa di Jeans. Un valore più preciso, si ottiene risolvendo le corrispondenti equazioni fluidodinamiche (cfr. Cosmology), ottenendo:

Ricercando soluzioni del tipo onda piana delle predette equazioni, si ha con ovvio significato dei simboli:

dove k è il vettore di propagazione:

e ω la pulsazione, che è data da

da cui vediamo che ω è reale se e solo se λ < λ_J. Diversamente, assume valori immaginari, e la fluttuazione si scrive:

ovvero un'onda stazionaria. Ne concludiamo che se le dimensioni corporee di A sono tali che le sue corde vocali generano una fluttuazione definita in un dominio λ > λ_J, le sue parole non giungeranno mai a B.

Tags: giganti, lunghezza d'onda di Jeans, onde sonore

Articoli correlati