[¯|¯] Il Principio antropico e l'altezza dei giganti
Ottobre 23rd, 2018 | by Marcello Colozzo |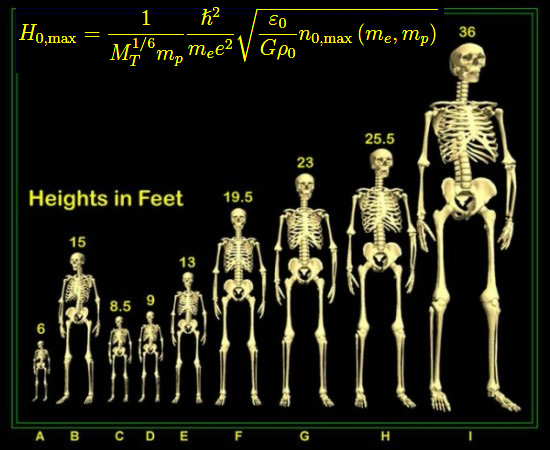
Nel post precedente abbiamo stabilito la seguente formula:
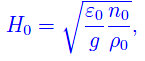
dove
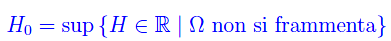
Cioè H0 è l'estremo superiore dell'insieme dei valori dell'altezza H di Ω (= organismo vivente) per i quali quest'ultimo conserva la propria integrità. Per valori maggiori, l'energia meccanica (cinetica+potenziale (gravitazionale)) è maggiore dell'energia di coesione che "tiene unite" le particelle (atomi/molecole) che compongono la superficie di Ω. Assegnato il valore di H, possiamo determinare il massimo valore della velocità con cui può traslare Ω senza frammentarsi. Avevamo trovato:
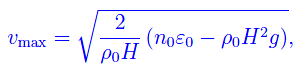
dove: ρ0 è la densità media di Ω, n0 è la concentrazione media delle coppie di particelle della superficie di Ω che ne garantiscono l'integrità attraverso un'energia di coesione di singola coppia pari a ε0. Esprimendo n0 in funzione di H0:
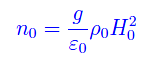
Possiamo poi approssimare
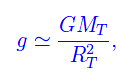
dove G è la costante di gravitazione universale, mentre MT e RT sono rispettivamente la massa e il raggio terrestre. Quindi
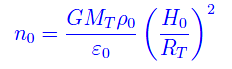
D'altra parte il raggio terrestre dipende da alcune costanti fisiche fondamentali (cfr. La creazione dell'universo)
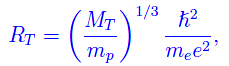
dove: h (tagliato) è la costante ridotta di Planck, me,e sono rispettivamente massa e carica dell'elettrone, ed mp è la massa del protone. Anche n0 dipende in qualche modo da me,mp, per cui ritenendo ε0 approssimativamente indipendente dalle predette costanti, si ha:
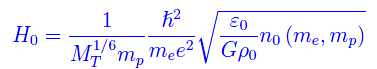
A sua volta n0 non può assumere valori arbitrariamente elevati, giacché dipende anche dalle distanze interatomiche, per cui potrà assumere al più un valore massimo n0,max(me,mp), a cui corrisponde un massimo valore per H0
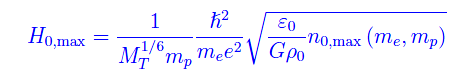
Ne concludiamo che la massima altezza raggiungibile da un organismo vivente, dipende da alcune costanti fisiche fondamentali e quindi, in ultima istanza, dal Principio antropico.
Tags: costanti fisiche fondamentali, energia di coesione, giganti, principio antropico
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











