» Esercizi svolti di Matematica e Fisica

[¯|¯] Le violente oscillazioni della parte reale e della parte immaginaria della zeta di Riemann

Forse l' analisi di Fourier potrebbe dirci qualcosa sulla congettura di Riemann. Ci riferiamo in particolare alle rapide oscillazioni della parte reale e della parte immaginaria della restrizione della funzione zeta lungo la linea critica. Le oscillazioni sono infatti dovute a termini del tipo n^-it, come mostrato nella figura al top. Nella figura seguente, invece, riportiamo il grafico di alcuni termini della serie di Dirichlet:

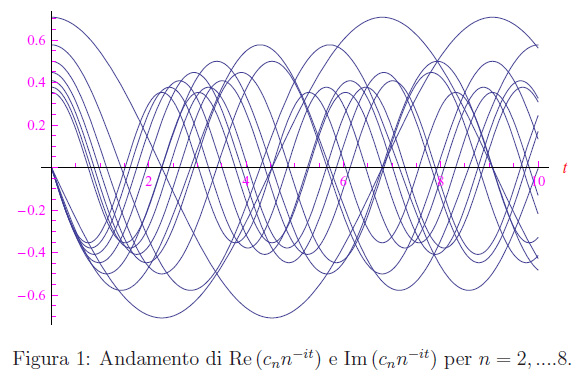
I conti sono qui

Tags: congettura di riemann, fourier, zeri non banali, zeta di riemann