[¯|¯] Integrazione numerica di un’equazione differenziale del primo ordine

[¯|¯] Integrazione numerica di un'equazione differenziale del primo ordine

Luglio 26th, 2017 | by Marcello Colozzo |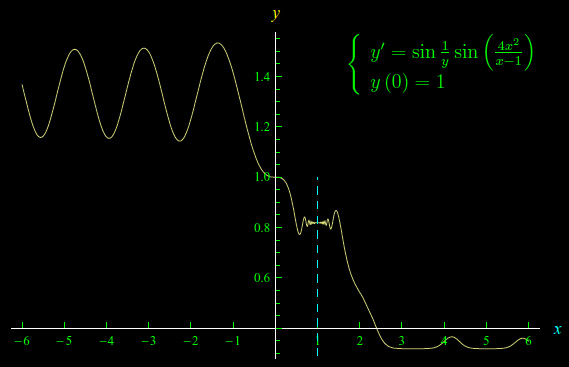

equazioni differenziali,integrazione numerica — **Fig. 1.**

Abbiamo esaminato fino ad ora equazioni differenziabili integrabili per quadrature, ovvero tramite il calcolo di un integrale. Ciò è possibile in tutti e soli i casi in cui sono coinvolte funzioni elementarmente esprimibili. Diversamente, l'equazione va integrata numericamente. Consideriamo, ad esempio, l'equazione differenziale:

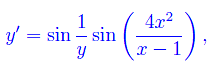
Soluzione
L'equazione assegnata è a variabili separabili ed è priva di integrali costanti giacché

Separiamo quindi le variabili
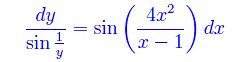
equazioni differenziali,integrazione numerica

Integriamo primo e secondo membro:

che non sono esprimibili nemmeno con le funzioni speciali della fisica matematica. Per procedere a una integrazione numerica, impostiamo il problema di Cauchy

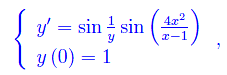
osservando nel frattempo che il grafico di sin(4x²)/(x-1)) compie infinite oscillazioni che non si smorzano, intorno al punto x=1. E ci aspettiamo un comportamento simile per l'integrale particolare che risolve il predetto problema di Cauchy. Infatti, integrando numericamente con mathematica otteniamo l'andamento riportato in fig. 1.

Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

v

Indice delle lezioni

No TweetBacks yet. (Be the first to Tweet this post)