» Esercizi svolti di Matematica e Fisica

[¯|¯] L'oscillatore anarmonico

Marzo 19th, 2017 | by Marcello Colozzo |

La seguente animazione è la traiettoria del punto rappresentativo di un oscillatore armonico nello spazio delle configurazioni lontano dalla risonanza.

Ques'altra animazione è, invece, la traiettoria del punto rappresentativo di un oscillatore anarmonico nello spazio delle fasi in condizioni di risonanza.

In un oscillatore anarmonico, la forza elastica anziché essere lineare in funzione della deformazione x della molla, segue una legge di potenza:

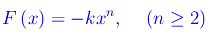
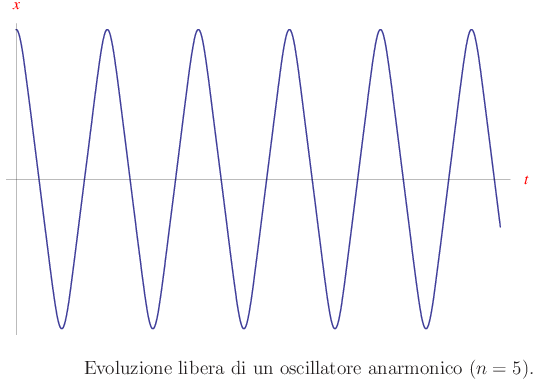
Abbiamo, dunque, un'equazione differenziale del second'ordine non lineare. La non linearità implica un'integrazione numerica. Ad esempio, per n=5 troviamo la soluzione plottata in figura:

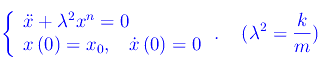
Naturalmente in questo caso la costante k>0 ha dimensioni diverse dalla costante elastica in regime lineare. Il secondo principio della dinamica nel caso di oscillazioni libere si traduce nel seguente problema di Cauchy:

Più interessante è il caso delle oscillazioni forzate. Ad esempio, applicando una forza

si ha:









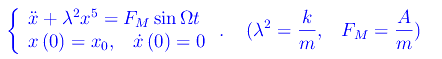
Formalmente, la condizione di risonanza si ottiene uguagliando i valori di λ e Ω tenendo conto che si tratta di grandezze dimensionalmente differenti. Ponendo tali grandezze pari a 20 (nelle appropriate unità di misura), compare l'animazione posta all'inizio di questo post, subito dopo l'orbita dell'oscillatore armonico. Troviamo, quindi, un andamento molto irregolare.

Concludiamo osservando che non è poi così irrealistico considerare oscillatori anarmonici. Infatti, molti processi di oscillazione sono in realtà non lineari. Ad esempio, nel caso dell'equazione di D'Alembert si considera una sbarra omogenea schematizzata da un numero infinitamente grande di oscillatore armonici di lunghezza infinitesima. L'accoppiamento di tali oscillatori permette il realizzarsi di un fenomeno di propagazione ondosa regolato dalla predetta equazione. La linearità di tali oscillatori implica la linearità dell'equazione di D'Alembert che nello specifico, è un'equazione differenziale alle derivate parziali. Di contro, l'utilizzo di oscillatori anarmonici riproduce nella suddetta schematizzazione un fenomeno di propagazione ondosa non lineare quale ad esempio, il solitone che è soluzione di una equazione d'onda non lineare.

Tags: forza elastica, oscillatore anarmonico, oscillatore armonico, risonanza

Articoli correlati