[¯|¯] Dirac ha a disposizione infiniti pettini di ordine N

Febbraio 14th, 2017 | by Marcello Colozzo |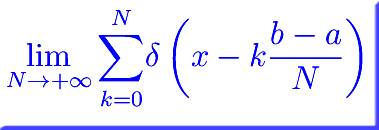

funzione delta di dirac,pettine di dirac,teoria delle distribuzioni,punto di accumulazione


Eseguiamo una decomposizione D([a,b]) di un intervallo [a,b] contenuto nell'insieme R dei numeri reali, ssegnando ad arbitrio N+1 punti, essendo N un intero naturale non nullo.

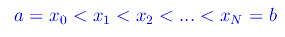
funzione delta di dirac,pettine di dirac,teoria delle distribuzioni,punto di accumulazione

La norma o ampiezza della decomposizione è il numero reale positivo:

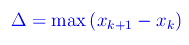
funzione delta di dirac,pettine di dirac,teoria delle distribuzioni,punto di accumulazione

Segue che [a,b] si decompone in N intervalli:

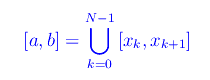
funzione delta di dirac,pettine di dirac,teoria delle distribuzioni,punto di accumulazione

Il numero di punti della decomposizione si esprime formalmente

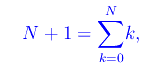
funzione delta di dirac,pettine di dirac,teoria delle distribuzioni,punto di accumulazione

dove δ(x-xk) è la funzione delta di Dirac centrata in xk. Quindi

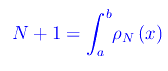
funzione delta di dirac,pettine di dirac,teoria delle distribuzioni,punto di accumulazione

Dal momento che

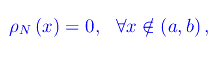
funzione delta di dirac,pettine di dirac,teoria delle distribuzioni,punto di accumulazione

si può scrivere:
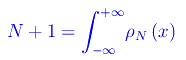
funzione delta di dirac,pettine di dirac,teoria delle distribuzioni,punto di accumulazione









Senza perdita di generalità, riferiamoci a una decomposizione di norma costante:

funzione delta di dirac,pettine di dirac,teoria delle distribuzioni,punto di accumulazione

cosicché
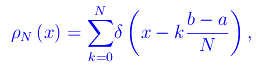
funzione delta di dirac,pettine di dirac,teoria delle distribuzioni,punto di accumulazione

da cui vediamo che le singole delte di Dirac si comportano da "segnaposto" per i singoli punti della decomposizione, e come tali enumerano i predetti punti. Infatti, troviamo N+1 delte di Dirac che compongono un pettine di Dirac di ordine N, come illustrato in figura:

funzione delta di dirac,pettine di dirac,teoria delle distribuzioni,punto di accumulazione

Fig. 1


Per N->+oo
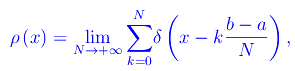
funzione delta di dirac,pettine di dirac,teoria delle distribuzioni,punto di accumulazione

essendo ρ(x) la densità del numero di punti di [a,b] ed è chiaro che

funzione delta di dirac,pettine di dirac,teoria delle distribuzioni,punto di accumulazione

giacché ogni punto di [a,b] è punto di accumulazione, per cui in ogni suo intorno cadono infiniti punti di [a,b] distinti da x. Ne concludiamo che l'operazione di passaggio al limite

funzione delta di dirac,pettine di dirac,teoria delle distribuzioni,punto di accumulazione

definisce un tentativo di enumerazione dei reali in [a,b] attraverso la generalizzazione al continuo di un pettine di Dirac di ordine N.

No TweetBacks yet. (Be the first to Tweet this post)

Tags: , , ,

Articoli correlati

Commenta l'esercizio