[¯|¯] Limite delle radici di un'equazione di secondo grado. Significato geometrico
Gennaio 30th, 2017 | by Marcello Colozzo |
Fig. 1
Discutere il comportamento delle radici dell'equazione di secondo grado
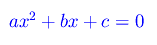
nel limite per a->0, supponendo b e c costanti, con b non nullo. Esprimere geometricamente il risultato ottenuto.
Soluzione
Le radici dell'equazione assegnata sono:

che possiamo esprimere in funzione di a:
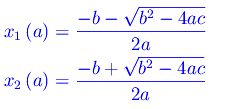
Più precisamente, per tutti i valori della variabile reale a tali che b²-4ac>0, le x1(a), x2(a) sono funzioni reali della variabile reale a, entrambe definite in R-{0}. Calcoliamo
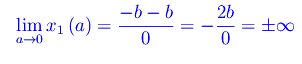
Segue

L'altra radice x2(a) si presenta nella forma indeterminata (0/0) che si risolve razionalizzando il numeratore:
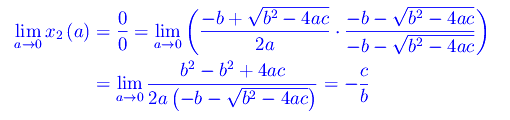
Interpretazione geometrica: la curva di equazione y=ax²+bx+c è una parabola, per cui le radici dell'equazione assegnata sono le ascisse dei punti di intersezione della parabola con l'asse x. Per a->0 la parabola tende alla retta y=bx+c che interseca l'asse x nel punto di ascissa -c/b, come illustrato in fig.1.
No TweetBacks yet. (Be the first to Tweet this post)
Tags: intersezioni con gli assi, limiti, parabola, radici equazione di secondo grado, retta
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











