[¯|¯] Forme differenziali e campi di forza conservativi
Novembre 3rd, 2016 | by Marcello Colozzo |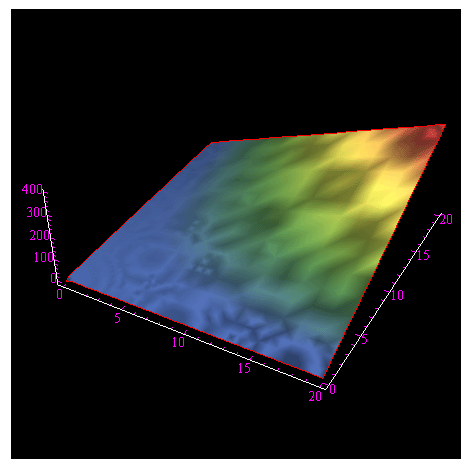
Andamento del potenziale da cui deriva il campo di forza dell'esercizio assegnato
Argomento di questo post è un'applicazione alla meccanica della nozione di forma differenziale lineare e conseguente integrale curvilineo. Più precisamente, consideriamo un campo di forza le cui componenti cartesiane sono assegnate funzioni continue X(x,y), Y(x,y), Z(x,y) in un dato campo semplicemente connesso. Come è noto, in tal caso la condizione di integrabilità si esprime attraverso una relazione di uguaglianza tra la derivata parziale di X rispetto a y, e la derivata parziale di Y rispetto a x.
Nel problema è assegnata una forma differenziale lineare Xdx+Ydy e si tratta, di stabilire se è un differenziale esatto. È chiaro che se la risposta è affermativa, il campo di forze assegnato è conservativo. Ed è abbastanza semplice calcolarne il potenziale.
Scarica l'esercizio completo in pdf
Tags: campi di forza conservativi, differenziale esatto, forme differenziali lineari, gradiente, potenziale
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











