Diodi in serie
Dicembre 2nd, 2022 | by Marcello Colozzo |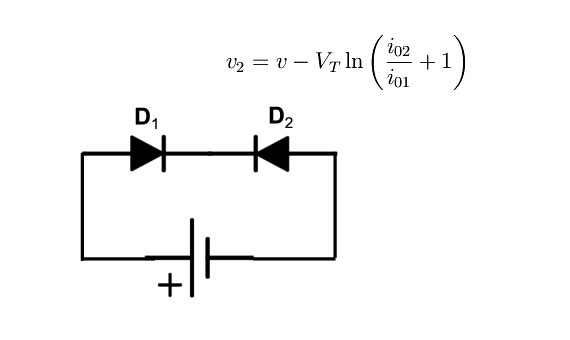
Esercizio
(Il testo è preso da Millman - Halkias. La soluzione è nostra)
(a) Due diodi p-n al germanio sono connessi in serie in direzione opposta all'altro (fig. 1 ). A questa combinazione serie viene applicata una batteria di 5V . Trovare la tensione che si localizza, alla temperatura ambiente, ai capi di ciascuna giunzione, supponendo che il valore della tensione di Zener sia superiore a 5V .
Si noti come il risultato sia indipendente dalla corrente di saturazione inversa. È anche indipendente dalla temperatura?
(b) Se il valore della tensione di Zener è 4.9V , quanto varrà l'intensità della corrente che scorre nel circuito? L'intensità della corrente di saturazione inversa sia 5µA .
Soluzione
Quesito (a). Quesito (a). Se v1 e v2 sono rispettivamente le tensioni ai capi delle giunzioni, per il secondo principio di Kirchhoff si ha:
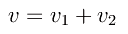
Siccome D2 è in polarizzazione inversa, l'unica corrente che può circolare nella serie è la corrente di saturazione inversa di D2 che denotiamo con i02. Ne segue dalla caratteristica tensione-corrente di D1
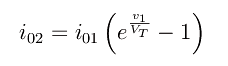
dove i01 è la corrente di saturazione inversa di D1, mentre come già sappiamo a temperatura ambiente l'equivalente in volt della temperatura vale:
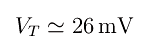
Dall'equazione più sopra ricaviamo
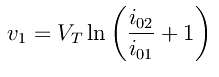
e quindi da Kirchhoff:
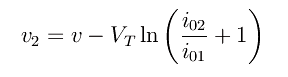
Riguardo all'indipendenza dalla corrente di saturazione inversa, la risposta è affermativa solo se i diodi sono identici, e dal testo si evince proprio questa circostanza. In tal caso si ha
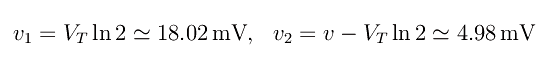
Quesito (b). Trovandosi D2 in breakdown, la differenza di potenziale ai sui capi non può essere che vZ=4.9V , da cui v1=v-vZ=0.1V . Ciò forza il diodo D1 a far circolare una corrente
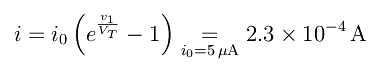



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











