Raddrizzatore a semplice semionda con filtro capacitivo (parte 2) |

Raddrizzatore a semplice semionda con filtro capacitivo (parte 2)

Novembre 29th, 2022 | by Marcello Colozzo |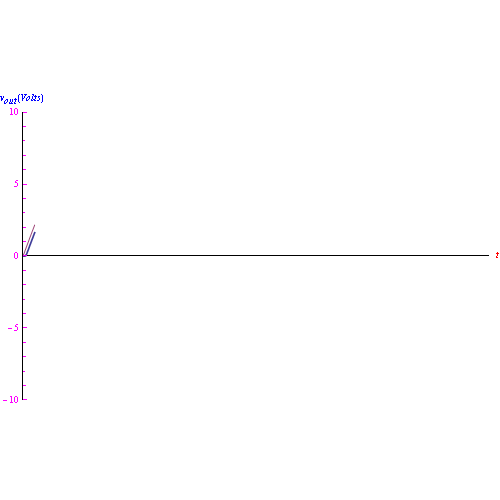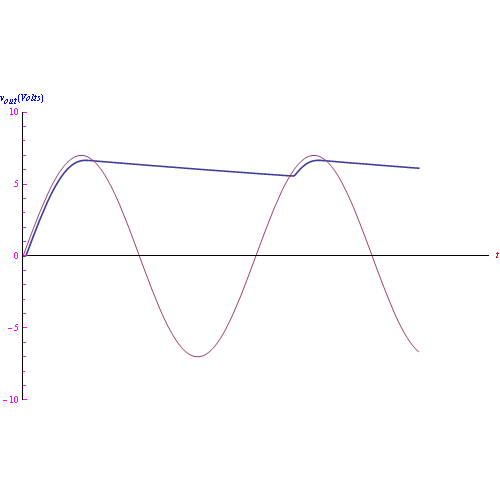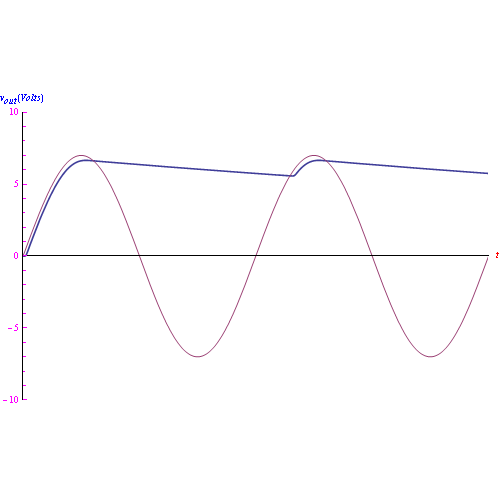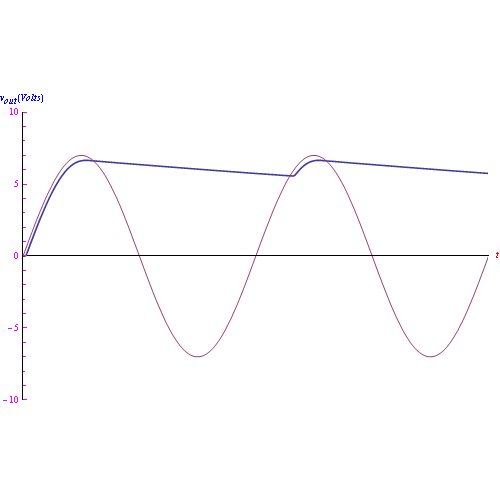

resistenza, condensatore, diodo,filtro capacitivo — **Fig. 1.**

Riferiamoci allo schema più realistico

Applichiamo i principi di Kirchhoff:
Nodo N:

Maglia 1:

dove possiamo porre η=1 assumendo un diodo al germanio. V(T) è l'equivalente in volt della temperatura di equilibrio termodinamico del diodo:

>Maglia 2:

>Maglia 3:

Definiamo le seguenti funzioni incognite:

Combinando le varie equazioni si giunge

Supponiamo di lavorare con un diodo che ha i₀=1µA , quindi utilizziamo un condensatore elettrolitico da 1µF . Riguardo alla resistenza di carico per quanto visto nell'esperienza precedente, deve essere RC»f^-1, ad esempio R=10²kΩ. Segue

dove abbiamo specificato la condizione iniziale di condensatore inizialmente scarico. Abbiamo scritto un'equazione differenziale del primo ordine in x₂(t) di forma non normale. Ciò non è un problema se si integra numericamente, tuttavia integrando alla cieca, cioè così com'è, il software Mathematica và in overflow per la presenza di «numeri molto grandi». Presumibilmente, il software passa dal logaritmo agli esponenziali, e da qui l'overflow. Nel frattempo svincoliamoci dal logaritmo:

e qui scopriamo che è proprio il termine V(T) a creare overflow per via del valore «troppo piccolo» per T=300K . Dopo vari tentativi, vediamo che la minima temperatura per la quale è possibile l'integrazione con Mathematica, è 800K . È chiaro che un tale valore oltre ad essere non realistico, distrugge la validità del modello di diodo nei temini di caratteristica tensione-corrente. In parole povere, non è più valida l'equazione differenziale che stiamo risolvendo. Ciò comunque và considerato come un artificio matematico per l'integrazione dell'equazione medesima.
Nel grafico di fig. 1 riportiamo il risultato dell'integrazione numerica, cioè la tensione di uscita, da cui notiamo il processo di scarica del condensatore. Ci rimane l'altra funzione incognita x1(t) i.e. la corrente nel ramo resistitivo, e a questo punto calcoliamo la corrente nel diodo: