» Esercizi svolti di Matematica e Fisica

Ampiezza di correlazione, e relazione di indeterminazione tempo-energia

Dicembre 14th, 2021 | by Marcello Colozzo |

---

Sia S_q un sistema quantistico non relativistico, il cui stato inziale è |ψ₀> vettore ket dello spazio di Hilbert associato al sistema. Supponendo che l'hamiltoniano H non dipenda esplicitamente dal tempo, l'operatore di evoluzione è semplicemente dato da:

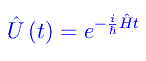
Ne segue che lo stato quantistico del sistema è a tutti i tempi:

Definizione
Dicesi ampiezza di correlazione la seguente funzione della variabile reale t:

Si noti che è una funzione da R a C il cui modulo ci dà un'informazione su come lo stato a un generico istantet è correlato allo stato iniziale. Infatti:

cioè la massima correlazione. Inoltre tale funzione può essere scritta come

Senza perdita di generalità, supponiamo che lo spettro dell'hamiltoniano sia puramente discreto e non degenere:

per cui abbiamo l'equazione agli autovalori:

Se lo stato iniziale è un autostato dell'energia:

Si ha

Ed è ovvio perché lo stato iniziale è uno stato stazionario. Diversamente

Segue

Quindi

La delta di Kronecher cancella tutti i termini della doppia sommatoria con n=n, quindi otteniamo finalmente l'espressione dell'ampiezza di correlazione a tutti i tempi:

Da qui vediamo che a tempi lunghi si realizzano violente oscillazioni dei singoli termini con frequenze E_n/h e conseguenti cancellazioni delle somme dei termini medesimi. Per essere più quantitativi, siccome non siamo in grado di valutare la somma, eseguiamo una qualche possibile stima. Innanzitutto consideriamo il limite per N->+oo, per cui abbiamo una serie (v. fig. 1). Il modo più efficace consiste nel poter rimpiazzare la sommatoria con un integrale, il che si traduce nell'approssimare lo spettro discreto dell'hamiltoniano con uno spettro continuo, a patto di avere una distribuzione di autovalori sufficientemente densa:

E possiamo sempre porre E₀=0 giacché lo zero dell'energia lo possiamo piazzare dove ci pare (l'energia è definita a meno di una inessenziale costante additiva). I coefficienti complessi c_n° verranno sostituiti da una funzione γ°(E). Un'eventuale degenerazione dello spettro dell'hamiltoniano si traduce in una densità degli stati. Infatti, ricordiamo che l'autovalore E_n è degenere g_n > 1 volte, se ad esso corrispondono g_n autovettori linearmente indipendenti. Fisicamente, significa che esistono g_n stati quantici distinti con lo stesso autovalore. Nel continuo possiamo dunque avere dN(E) stati di energia tra E e E+dE, e quindi una densità degli stati, i.e. numero di stati per intervallo unitario di energia:

Ne segue

dove

che verifica la condizione di normalizzazione:

L'integrale può essere stimato eseguendo ragionevoli assunzioni sulla funzione f(E). Abbiamo considerato idealmente uno stato iniziale quale sovrapposizione lineare di infiniti autostati dell'energia. Sperimentalmente, è più realistico preparare il sistema in una sovrapposizione di un numero limitato di autostati. Nel continuo ciò si traduce con una f(E) estremamente "piccata" intorno a un valore E e con larghezza ΔE. Abbiamo

Per quanto discusso sull'andamento di f(E), si ha che il contributo dominante all'integrale proviene da E in [E-ΔE,E+ΔE]. Osserviamo che a tempi t tali che

non si ha contributo apprezzabile a C(t) a causa della cancellazione dei singoli termini. Diversamente, dobbiamo attendere un tempo t tale che

che definisce la ben nota relazione di indeterminazione tempo-energia.

Articoli correlati